题目内容
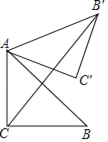
【题目】如图，在△ABC中，∠ACB＝90°，AC＝BC＝
，将△ACB绕点A逆时针旋转60°得到△AC′B′，则CB′的长为（ ）
A. +
B. 1+
C. 3D. +
【答案】B
【解析】
连接BB'，根据线段垂直平分线的判定定理可得：CB'是AB的垂直平分线，则CB'⊥AB，AF＝BF，分别计算CF和B'F的长，相加可得结论．
连接BB'，设CB'与AB的交点为F，
由旋转得：AB＝AB'，∠BAB'＝60°，
∴△ABB'是等边三角形，
∴AB'＝BB'，
∵AC＝BC，
∴CB'是AB的垂直平分线，
∴CB'⊥AB，AF＝BF，
Rt△ACB中，AC＝BC＝
，
∴AB＝2，CF＝
AB＝1，
∵BB'＝AB＝2，BF＝1，
由勾股定理得：B'F＝
，
∴CB'＝CF+B'F＝1+
，
故选：B．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
【题目】某中学举行“校园朗读者”朗诵大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．
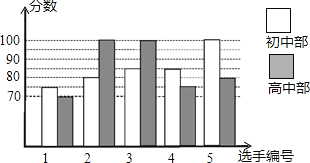
（1）根据图示填写表格；
平均分（分） | 中位数（分） | 众数（分） | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
（2）结合两队成绩的平均数和中位数， 队的决赛成绩较好；
（3）已知高中代表队决赛成绩的方差为160，计算初中代表队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．（方差公式：S2＝
[（x1﹣
）2+（x2﹣）2+…+（xn﹣）2]
