题目内容
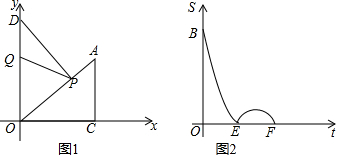
20. 如图,OE平分∠AOB,EF∥OB,EC⊥OB.
如图,OE平分∠AOB,EF∥OB,EC⊥OB.(1)求证:OF=EF
(2)若∠BOE=15°,EC=5求:OF的值.
分析 (1)根据角平分线的定义得到∠BOE=∠AOE,由平行线的性质得到∠BOE=∠OEF,等量代换得到∠OEF=∠FOE,于是得到结论;
(2)过E作ED⊥OA于D,根据三角形的外角的性质得到∠EFD=30°,根据直角三角形的性质即可得到结论.
解答 (1)证明:∵OE平分∠AOB,
∴∠BOE=∠AOE,
∵EF∥OB,
∴∠BOE=∠OEF,
∴∠OEF=∠FOE,
∴OF=EF;
(2)解: 过E作ED⊥OA于D,
过E作ED⊥OA于D,
∵∠BOE=15°,
∴∠OEF=∠FOE=15°,
∴∠EFD=30°,
∵CE⊥OB,
∴DE=CE=5,
∴EF=2DE=10,
∴OF=EF=10.
点评 本题考查了角平分线的性质,直角三角形的性质,平行线的性质,等腰三角形的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
相关题目
9.若|x|=3,|y|=4,且|x-y|=y-x,则xy的值为( )
| A. | -1 | B. | -12 | C. | 12 | D. | 12或-12 |
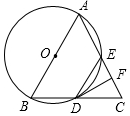 如图,已知在△ABC中,AB=AC=13,BC=10,以AB为直径作⊙O,交BC于D,交AC于E,DF⊥CE,垂足为F
如图,已知在△ABC中,AB=AC=13,BC=10,以AB为直径作⊙O,交BC于D,交AC于E,DF⊥CE,垂足为F