题目内容
已知抛物线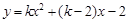 (其中
(其中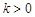 ).
).
1.(1)求该抛物线与x轴的交点坐标及顶点坐标(可以用含k的代数式表示);
2.(2)若记该抛物线的顶点坐标为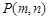 ,直接写出
,直接写出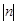 的最小值;
的最小值;
3.(3)将该抛物线先向右平移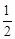 个单位长度,再向上平移
个单位长度,再向上平移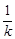 个单位长度,随着
个单位长度,随着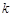 的变化,平移后的抛物线的顶点都在某个新函数的图象上,求这个新函数的解析式(不要求写自变量的取值范围).
的变化,平移后的抛物线的顶点都在某个新函数的图象上,求这个新函数的解析式(不要求写自变量的取值范围).
【答案】
1.解:(1)令 ,则
,则  .
.
整理,得  .
.
解得  ,
, .
.
∴ 该抛物线与x轴的交点坐标为 ,
, . ………………………2分
. ………………………2分
抛物线 的顶点坐标为
的顶点坐标为
2.(2)|n|的最小值为 2 .
3.(3)平移后抛物线的顶点坐标为 .…………………………………5分
.…………………………………5分
由 可得
可得  .
.
∴ 所求新函数的解析式为 .
.
【解析】略

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
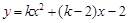 (其中
(其中 ).
).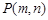 ,直接写出
,直接写出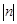 的最小值;
的最小值;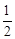 个单位长度,再向上平移
个单位长度,再向上平移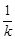 个单位长度,随着
个单位长度,随着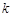 的变化,平移后的抛物线的顶点都在某个新函数的图象上,求这个新函数的解析式(不要求写自变量的取值范围).
的变化,平移后的抛物线的顶点都在某个新函数的图象上,求这个新函数的解析式(不要求写自变量的取值范围).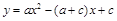 (其中a ≠ c且a ≠0).
(其中a ≠ c且a ≠0).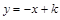 与此抛物线的另一个交点为
与此抛物线的另一个交点为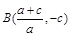 ,求此抛物线的解析式;
,求此抛物线的解析式; ,求点P的坐标;
,求点P的坐标;