题目内容
16.11月读书节,深圳市为统计某学校初三学生读书状况,如下图:(1)三本以上的x值为20%,参加调查的总人数为400,补全统计图;
(2)三本以上的圆心角为72°.
(3)全市有6.7万学生,三本以上有13400人.
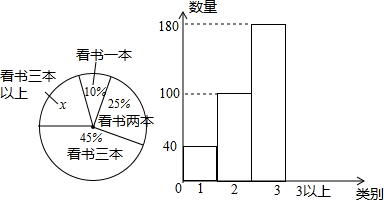
分析 (1)根据看1本书的人数为40人,所占的百分比为10%,40÷10即可求出总人数,用100%-10%-25%-45%即可得x的值,用总人数乘以x的值,即可得到3本以上的人数,即可补全统计图;
(2)用x的值乘以360°,即可得到圆心角;
(3)用6.7万乘以三本以上的百分比,即可解答.
解答 解:(1)40÷10%=400(人),
x=100%-10%-25%-45%=20%,400×20%=80(人),
故答案为:20%,400;
如图所示;
(2)20%×360°=72°,
故答案为:72°;
(3)67000×20%=13400(人),
故答案为:13400.
点评 此题主要考查了条形图与扇形图的综合应用,解决此类问题注意图形有机结合,综合分析获取正确信息.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
11. 八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”
八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”
四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
(1)计算m=40;
(2)在扇形统计图中,“其他”类所占的百分比为15%;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是乙和丙的概率.
 八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”
八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
| 类别 | 频数(人数) | 频率 |
| 小说 | 0.5 | |
| 戏剧 | 4 | |
| 散文 | 10 | 0.25 |
| 其他 | 6 | |
| 合计 | m | 1 |
(2)在扇形统计图中,“其他”类所占的百分比为15%;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是乙和丙的概率.
1. 二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )
 二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关系式错误的是( )| A. | a<0 | B. | b>0 | C. | b2-4ac>0 | D. | a+b+c<0 |
8.下列计算中,不正确的是( )
| A. | -2x+3x=x | B. | 6xy2÷2xy=3y | C. | (-2x2y)3=-6x6y3 | D. | 2xy2•(-x)=-2x2y2 |
10.长沙黄花国际机场进一步扩建,其建筑面积约26万平方米,将26万平方米用科学记数法表示为( )
| A. | 26×104平方米 | B. | 2.6×104平方米 | C. | 2.6×105平方米 | D. | 2.6×106平方米 |
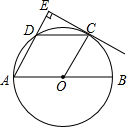 如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E. 如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).
如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1). 如图,一个几何体是由两个小正方体和一个圆锥构成,其主视图是( )
如图,一个几何体是由两个小正方体和一个圆锥构成,其主视图是( )


