题目内容
 如图所示,EF分别与AB,CD相交于N,M,∠EMC=50°,∠ENB=130°,那么( )
如图所示,EF分别与AB,CD相交于N,M,∠EMC=50°,∠ENB=130°,那么( )分析:A、从两直线平行与相交的关系来判断正误;
B、利用同位角∠ENB=∠END=130°,推知两直线AB∥CD;
C、D利用反证法证明.
B、利用同位角∠ENB=∠END=130°,推知两直线AB∥CD;
C、D利用反证法证明.
解答: 解:延长AE、FD交与点G.
解:延长AE、FD交与点G.
A、∵AE与DE相交于点E,∴它们不可能平行;故本选项错误;
B、∵∠EMC=50°,
∴∠EMD=130°(平角的定义);
而∠ENB=130°,
∴∠ENB=∠END=130°,
∴AB∥CD(同位角相等,两直线平行);
故本选项正确;
C、∵AB∥CD(由B项证明),
∴∠GCD=∠A(两直线平行,同位角相等);
若∠A=∠D时,则∠GCD=∠A,
∴AG∥FD,这与AE、FD相交矛盾;
故本选项错误;
D、若∠E=∠F时,则AG∥FD,
这与AE、FD相交矛盾;
故本选项错误.
故选B.
 解:延长AE、FD交与点G.
解:延长AE、FD交与点G.A、∵AE与DE相交于点E,∴它们不可能平行;故本选项错误;
B、∵∠EMC=50°,
∴∠EMD=130°(平角的定义);
而∠ENB=130°,
∴∠ENB=∠END=130°,
∴AB∥CD(同位角相等,两直线平行);
故本选项正确;
C、∵AB∥CD(由B项证明),
∴∠GCD=∠A(两直线平行,同位角相等);
若∠A=∠D时,则∠GCD=∠A,
∴AG∥FD,这与AE、FD相交矛盾;
故本选项错误;
D、若∠E=∠F时,则AG∥FD,
这与AE、FD相交矛盾;
故本选项错误.
故选B.
点评:本题考查了平行线的判定与性质.解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
相关题目
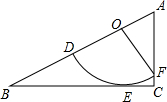 如图所示为扇形DOF与直角△ABC的重迭情形,其中O,D,F分别在AB,OB,AC上,且
如图所示为扇形DOF与直角△ABC的重迭情形,其中O,D,F分别在AB,OB,AC上,且
 25、友情提示:本题有A、B两题,请你任选一题作答,A题满分9分,B题满分12分.若两题都做,只能按A题评分.
25、友情提示:本题有A、B两题,请你任选一题作答,A题满分9分,B题满分12分.若两题都做,只能按A题评分.
 如图所示,EF过平行四边形ABCD对角线的交点O,且分别交AD、BC于点E、F,若平行四边形ABCD的面积为12,则△AOE与△BOF的面积之和等于( )
如图所示,EF过平行四边形ABCD对角线的交点O,且分别交AD、BC于点E、F,若平行四边形ABCD的面积为12,则△AOE与△BOF的面积之和等于( ) 如图所示,EF分别与AB,CD相交于N,M,∠EMC=50°,∠ENB=130°,那么
如图所示,EF分别与AB,CD相交于N,M,∠EMC=50°,∠ENB=130°,那么