题目内容
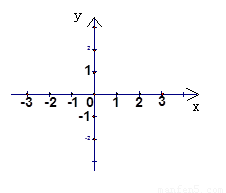
如图，A、B、C是二次函数y=ax2+bx+c（a≠0）的图象上的三点．根据图中给出的三点的位置情况，可得a、c、△（△=b2-4ac）与零的大小关系是：a________0，c________0，△________0．（填入“＞”、“＜”或“=”）
＜ ＜ ＞
分析：根据二次函数图象的开口方向来判断a的符号；由图象与y轴的交点来判断c的符号；根据图象与x轴交点的个数来判断根的判别式的符号．
解答：画草图得，此函数开口向下，所以a＜0；
与与y轴的交点为在y轴的负半轴上，所以c＜0；
抛物线与x轴有两个交点，∴b2-4ac＞0．
故答案是：＜、＜、＞．
点评：本题考查了二次函数图象与系数的关系．解题的关键是灵活应用数形结合思想．
分析：根据二次函数图象的开口方向来判断a的符号；由图象与y轴的交点来判断c的符号；根据图象与x轴交点的个数来判断根的判别式的符号．
解答：画草图得，此函数开口向下，所以a＜0；
与与y轴的交点为在y轴的负半轴上，所以c＜0；
抛物线与x轴有两个交点，∴b2-4ac＞0．
故答案是：＜、＜、＞．
点评：本题考查了二次函数图象与系数的关系．解题的关键是灵活应用数形结合思想．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
19、如图，A，B，C是二次函数y=ax2+bx+c（a≠0）的图象上三点，根据图中给出的三点的位置，可得a
12、如图，A、B、C是二次函数y=ax2+bx+c（a≠0）的图象上的三点．根据图中给出的三点的位置情况，可得a、c、△（△=b2-4ac）与零的大小关系是：a
的两个解。
__________的图象与
轴交点的横坐标，即
，
就是方程的解。
的两个解。
__________的图象与
轴交点的横坐标，即
，
就是方程的解。
