题目内容
【阅读】在平面直角坐标系中,以任意两点p(x1,y1)、Q(x2,y2)为端点的线段中点坐标为(
,
)
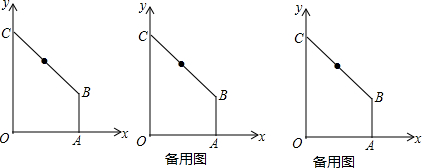
【运用】已知:如图,在直角梯形COAB中,OC∥AB,∠AOC=90°,AB=4,AO=8,OC=10,以O为原点建立平面直角坐标系,点D为线段BC的中点,动点P从点A出发,以每秒4个单位的速度,沿折线AOCD向终点C运动,运动时间是t秒.
(1)D点的坐标为 ;
(2)当t为何值时,△APD是直角三角形;
(3)点P移动过程中,设△OPD的面积为S,请直接写出S与t的函数关系式,并指出自变量t的取值范围;
(3)如果另有一动点Q,从C点出发,沿折线CBA向终点A以每秒5个单位的速度与P点同时运动,当一点到达终点时,两点均停止运动,问:P、C、Q、A四点围成的四边形的面积能否为28?如果可能,求出对应的t;如果不可能,请说明理由.
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
【运用】已知:如图,在直角梯形COAB中,OC∥AB,∠AOC=90°,AB=4,AO=8,OC=10,以O为原点建立平面直角坐标系,点D为线段BC的中点,动点P从点A出发,以每秒4个单位的速度,沿折线AOCD向终点C运动,运动时间是t秒.
(1)D点的坐标为
(2)当t为何值时,△APD是直角三角形;
(3)点P移动过程中,设△OPD的面积为S,请直接写出S与t的函数关系式,并指出自变量t的取值范围;
(3)如果另有一动点Q,从C点出发,沿折线CBA向终点A以每秒5个单位的速度与P点同时运动,当一点到达终点时,两点均停止运动,问:P、C、Q、A四点围成的四边形的面积能否为28?如果可能,求出对应的t;如果不可能,请说明理由.

考点:一次函数综合题
专题:
分析:(1)坐标系中线段中点的坐标等于线段两端点坐标和的一半;
(2)分两种情况,DP垂直AP或PD垂直DA,根据勾股定理,可得答案;
(3)分类讨论:0<t<2,2<t<
时,根据三角形的面积公式,可得答案;
(4)利用已知条件可求BC=10,直角梯形COAB的面积=56.假设P、C、Q、A四点围成的四边形的面积为28,由于动点P从点A出发到达点O时,用时2秒,此时从C点出发的点Q恰好到达点B,P、C、Q、A四点围成的四边形即为直角梯形COAB,所以t=2秒时四边形的面积不能为28.分两种情况:t<2,t>2.
(2)分两种情况,DP垂直AP或PD垂直DA,根据勾股定理,可得答案;
(3)分类讨论:0<t<2,2<t<
| 9 |
| 2 |
(4)利用已知条件可求BC=10,直角梯形COAB的面积=56.假设P、C、Q、A四点围成的四边形的面积为28,由于动点P从点A出发到达点O时,用时2秒,此时从C点出发的点Q恰好到达点B,P、C、Q、A四点围成的四边形即为直角梯形COAB,所以t=2秒时四边形的面积不能为28.分两种情况:t<2,t>2.
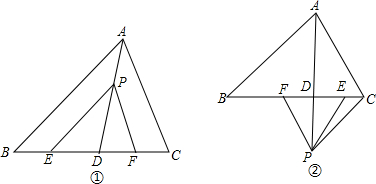
解答:解:(1)如图1:

∵AO=8,
∴从点D向OA引垂线,垂足为D1,OD1=4.从D向OC引垂线,垂足为D2.OD2=DD1=
(AB+CO)=7.
故D点的坐标是(4,7).
故答案为:(4,7);
(2)如图2:

直角三角形即能满足勾股定理.
则根据速度公式可得:当DP⊥AO,
点D为线段BC的中点,D点的坐标是(4,7).
∴AP=4,
t1=1,
利用勾股定理表示出AP12=82+(4t-8)2,AD2=42+72,P1D=2=42+(7-4t+8)2,
t2=
.
(3)S=
(4)解:存在对应的t,能够使P、C、Q、A四点围成的四边形的面积为28.理由如下:
由于t=2秒时,P、C、Q、A四点围成的四边形即为直角梯形COAB,
所以t=2秒时四边形的面积不能为28.
AP=4t,CQ=5t.
下面分两种情况分别讨论:如图3,

①t<2秒时,点P在边OA上,点Q在边BC上.
∵四边形PCQA的面积=28,
∴△POC的面积+△ABQ的面积=直角梯形COAB的面积-四边形PCQA的面积=28,
∴
×10×(8-4t)+
×4×
=28,
解得t=1.
∵1<2,
∴t=
符合题意;
如图4:

②t>2秒时,点P在边OC上,点Q在边AB上,四边形PCQA为梯形.
∵四边形PCQA的面积=28,
∴
(18-4t+14-5t)×8=28,
解得t=
.
∵
<
,
∴t=
符合题意.
故当t=1或
时,P、C、Q、A四点围成的四边形的面积为28.

∵AO=8,
∴从点D向OA引垂线,垂足为D1,OD1=4.从D向OC引垂线,垂足为D2.OD2=DD1=
| 1 |
| 2 |
故D点的坐标是(4,7).
故答案为:(4,7);
(2)如图2:

直角三角形即能满足勾股定理.
则根据速度公式可得:当DP⊥AO,
点D为线段BC的中点,D点的坐标是(4,7).
∴AP=4,
t1=1,
利用勾股定理表示出AP12=82+(4t-8)2,AD2=42+72,P1D=2=42+(7-4t+8)2,
t2=
| 89 |
| 28 |
(3)S=
|
(4)解:存在对应的t,能够使P、C、Q、A四点围成的四边形的面积为28.理由如下:
由于t=2秒时,P、C、Q、A四点围成的四边形即为直角梯形COAB,
所以t=2秒时四边形的面积不能为28.
AP=4t,CQ=5t.
下面分两种情况分别讨论:如图3,

①t<2秒时,点P在边OA上,点Q在边BC上.
∵四边形PCQA的面积=28,
∴△POC的面积+△ABQ的面积=直角梯形COAB的面积-四边形PCQA的面积=28,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 4(10-5t) |
| 5 |
解得t=1.
∵1<2,
∴t=
| 25 |
| 9 |
如图4:

②t>2秒时,点P在边OC上,点Q在边AB上,四边形PCQA为梯形.
∵四边形PCQA的面积=28,
∴
| 1 |
| 2 |
解得t=
| 25 |
| 9 |
∵
| 25 |
| 9 |
| 14 |
| 5 |
∴t=
| 25 |
| 9 |
故当t=1或
| 25 |
| 9 |
点评:本题考查梯形,坐标与图形性质,直角三角形的判定等,注意动态问题要考虑全面.

练习册系列答案
相关题目
下列判定两个三角形全等的说法中,不正确的是( )
| A、三角对应相等的两个三角形全等 |
| B、三边对应相等的两个三角形全等 |
| C、有一边及其对角和另一角对应相等的两个三角形全等 |
| D、有一组直角边对应相等的两个等腰直角三角形全等 |
若a=b,则下列式子正确的有( )
①a-2=b-2;②
a=
b;③-
a=-
b;④5a-1=5b-1.
①a-2=b-2;②
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在△SAB中,CD∥AB,AD,BC交于S点,AC,BD交于O点,SO与AB,CD分别交于N,M点,AN=BN,求证:DM=CM.
如图,在△SAB中,CD∥AB,AD,BC交于S点,AC,BD交于O点,SO与AB,CD分别交于N,M点,AN=BN,求证:DM=CM. 如图,将方格中的图形作下列运动,画出运动后的图形.
如图,将方格中的图形作下列运动,画出运动后的图形.