Question

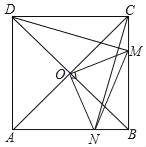
【题目】如图，已知为锐角内部一点，过点作于点，于点，以为直径作，交直线于点，连接，交于点.

（1）求证：.

（2）连接，当，时，在点的整个运动过程中.

①若，求的长.

②若为等腰三角形，求所有满足条件的的长.

（3）连接，交于点，当，时，记的面积为，的面积为，请写出的值.

Answer 1

【答案】（1）见解析；（2）①；②2，3或；(3)见解析；

【解析】

（1）根据垂直的定义得出∠ABP=∠ACP=90°，根据四边形的内角和得出∠BAC+∠BPC=180°，根据平角的定义得出∠BPD+∠BPC=180°，再根据同角的余角相等即可证明结论；

（2）①根据等腰直角三角形的性质得出BP=AB=2，根据等角的同名三角函数值相等及正切函数的定义得出BP=PD，从而得出PD的长；

②当BD=BE时，∠BED=∠BDE，故∠BPD=∠BPE=∠BAC，根据等角的同名三角函数值相等得出tan∠BPE=2，根据正切函数的定义，由AB=2得出BP=，根据勾股定理即可求出BD；

当BE=DE时，∠EBD=∠EDB，由∠APB=∠BDE，∠DBE=∠APC，得出∠APB=∠APC，则AC=AB=2，过点B作BG⊥AC于点G，得四边BGCD是矩形，根据正切函数的定义得出AG=2，进而可求出BD；

当BD=DE时，∠DEB=∠DBE=∠APC，由∠DEB=∠DPB=∠BAC得出∠APC=∠BAC，设PD=x，则BD=2x，根据正切函数的定义列出关于x的方程，求解得出x的值，进而由BD=2x得出答案；

（3），过点O作OH上DC于点H，根据tan∠BPD=tan∠MAN=1得出BD=DP，令BD=DP=2a，PC=2b得OH=a，CH=a+2b．AC=4a+2b，证△ACP∽△CHO得，据此得出a＝b及CP＝2a、CH＝3a、OC＝a，再根据△CPF∽△COH，

得，据此求得CF＝，OF＝，证OF为△PBE的中位线知EF＝PF，从而依据可得答案．

（1）解：

∵，

∴

∴

∵

∴

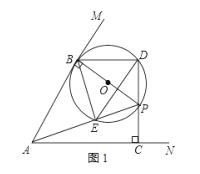
（2）解：①如图1，

∵

∴

∵

∴

∴

∴

∴

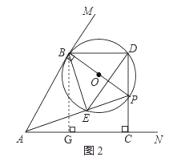
②如图2，当时，∴

∴

∵，∴

在中，，设，则，∴，解得

∴

当时，

∵

∴

∴

过点作于点，得四边形是矩形

∵，

∴

∴

当时，

∵

∴

设，则

∴，∴

∴，∴

综上所述，当为2，3或时，为等腰三角形.

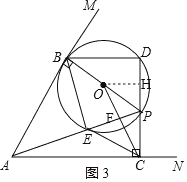
（3）如图3，过点O作OH⊥DC于点H，

∵tan∠BPD＝tan∠MAN＝1，

∴BD＝PD，

设BD＝PD＝2a、PC＝2b，

则OH＝a、CH＝a＋2b、AC＝4a＋2b，

∵OC∥BE且∠BEP＝90°，

∴∠PFC＝90°，

∴∠PAC＋∠APC＝∠OCH＋∠APC＝90°，

∴∠OCH＝∠PAC，

∴△ACP∽△CHO，

∴，即OHAC＝CHPC，

∴a（4a＋2b）＝2b（a＋2b），

∴a＝b，

即CP＝2a、CH＝3a，

则OC＝a，

∵△CPF∽△COH，

∴，即，

则CF＝，OF＝OCCF＝，

∵BE∥OC且BO＝PO，

∴OF为△PBE的中位线，

∴EF＝PF，

∴