��Ŀ����
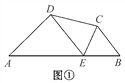
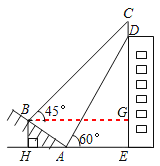
����Ŀ����ͼ��ij��¥�Ķ�������һ������CD��С����ɽ�µ��½�A����ù���Ƶײ�D������Ϊ60����������AB�����ߵ�B����ù���ƶ���C������Ϊ45������֪ɽ��AB���¶�i=1��![]() ��AB=10����AE=15������i=1��
��AB=10����AE=15������i=1��![]() ��ָ�����Ǧֱ�߶�BH��ˮƽ����AH�ıȣ�
��ָ�����Ǧֱ�߶�BH��ˮƽ����AH�ıȣ�

��1�����B��ˮƽ��AE�ĸ߶�BH��
��2��������CD�ĸ߶ȣ�
��������ĸ߶Ⱥ��Բ��ƣ������ȷ��0.1�����ο����ݣ�![]() 1.414��
1.414��![]() 1.732��
1.732��
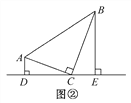
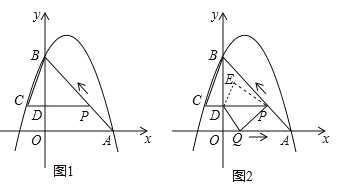
���𰸡��⣺��1����B��BG��DE��G��
��Rt��ABF��i=tan��BAH=![]() �����BAH=30��
�����BAH=30��
��BH=![]() AB=5��������
AB=5��������
�𣺵�B��ˮƽ��AE�ĸ߶�BHΪ5����
��2������1������BH=5��AH=5![]() ��
��
��BG=AH+AE=5![]() +15��
+15��
��Rt��BGC������CBG=45������CG=BG=5![]() +15��
+15��
��Rt��ADE������DAE=60����AE=15��
��DE=![]() AE=15
AE=15![]() ��
��
��CD=CG+GE��DE=5![]() +15+5��15
+15+5��15![]() =20��10
=20��10![]() ��2.7��������
��2.7��������
��������CD��Լ2.7����
��������
������1����B��DE�Ĵ��ߣ��费��ΪG���ֱ���Rt��ABH�У�ͨ����ֱ�����������BH��AH��
��2������ADE��ֱ�����������DE�ij������������EH��BG�ij�����Rt��CBG�У���CBG=45������CG=BG���ɴ˿����CG�ij�Ȼ�����CD=CG+GE��DE������������Ƶĸ߶ȡ���

����Ŀ��ij���˾���ӹ�˾�������ڶ������������·����������![]() �����ˣ���ʻ·�̼�¼����(�涨��Ϊ��������Ϊ������λ:
�����ˣ���ʻ·�̼�¼����(�涨��Ϊ��������Ϊ������λ:![]() ):
):
�� | �� | �� | �� | �� |
|
|
|
|
|
��1���������![]() �����˺ü�ʻԱ�ڹ�˾ʲô�����빫˾����ǧ��?
�����˺ü�ʻԱ�ڹ�˾ʲô�����빫˾����ǧ��?
��2�����ó��ÿǧ����![]() ������ô��������й����Ͷ�����?
������ô��������й����Ͷ�����?
��3�����ó���ļƼ۱�Ϊ����ʻ·�̲�����![]() �շ�
�շ�![]() Ԫ������
Ԫ������![]() �IJ��ְ�ÿǧ��
�IJ��ְ�ÿǧ��![]() Ԫ�շѣ���������иü�ʻԱ���յ����Ѷ���Ԫ?
Ԫ�շѣ���������иü�ʻԱ���յ����Ѷ���Ԫ?