题目内容
如图,两个反比例函数 和
和 (其中k1>k2>0)在第一象限内的图象依次是C1和
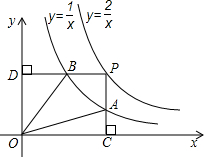
(其中k1>k2>0)在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( )
①△ODB与△OCA的面积相等;②四边形PAOB的面积等于k1-k2;
③PA与PB始终相等; ④当点A是PC的三等分点时,点B一定是PD三等分点.

A.①②
B.①②④
C.①④
D.①③④
【答案】分析:函数图象上的点和坐标轴构成的三角形的面积和四边形的面积和k是 和相等的关系,然后根据图象上的点确定线段的关系.
和相等的关系,然后根据图象上的点确定线段的关系.
解答:解:①△ODB与△OCA的面积都是 ,故①正确.
,故①正确.
②四边形OCPD的面积是k1,四边形PAOB的面积等于四边形OCPD的面积减去△ODB与△OCA的面积k1-k2.故②正确.
③当P位置改变后,PA与PB不一定 相等,故③不正确.
④因为P在C1上,A、B在C2上,所以当点A是PC的三等分点时,点B一定是PD三等分点,所以④正确.
故选B.
点评:本题考查反比例函数的综合运用,关键是知道函数图象上的点和坐标轴构成的三角形的面积和四边形的面积和k的关系.
 和相等的关系,然后根据图象上的点确定线段的关系.
和相等的关系,然后根据图象上的点确定线段的关系.解答:解:①△ODB与△OCA的面积都是
 ,故①正确.
,故①正确.②四边形OCPD的面积是k1,四边形PAOB的面积等于四边形OCPD的面积减去△ODB与△OCA的面积k1-k2.故②正确.
③当P位置改变后,PA与PB不一定 相等,故③不正确.
④因为P在C1上,A、B在C2上,所以当点A是PC的三等分点时,点B一定是PD三等分点,所以④正确.
故选B.
点评:本题考查反比例函数的综合运用,关键是知道函数图象上的点和坐标轴构成的三角形的面积和四边形的面积和k的关系.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图,两个反比例函数y=
如图,两个反比例函数y=| 2 |
| x |
| 1 |
| x |
| 2 |
| x |
| 1 |
| x |
| 1 |
| x |
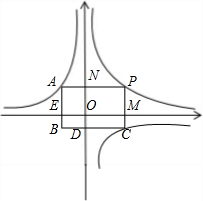 如图,两个反比例函数y=
如图,两个反比例函数y=| k1 |
| x |
| k2 |
| x |
| A、|k1-k2| | ||
B、
| ||
| C、|k1•k2| | ||
D、
|
 (2012•德州)如图,两个反比例函数
(2012•德州)如图,两个反比例函数 如图,两个反比例函数y=
如图,两个反比例函数y=