题目内容
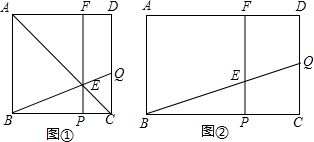
如图,已知矩形ABCD中,AB=4cm,BC=a厘米(a>4).动点P、Q同时从C点出发,点P在线段CB上以1厘米/秒的速度由C点向B点运动,点Q在线段CD上以相同的速度由C点向D点运动,过点P作直线垂直于BC,分别交BQ、AD于点E、F,当点Q到达终点D时,点P随之停止运动.设运动时间为t秒(t>0).(1)如图①,若a=5厘米,在运动过程中,当点E在矩形ABCD的对角线AC上时,求t的值;
(2)如图②,若a=6厘米,在运动过程中,是否存在某一时刻t,使得∠BFQ=90°?若存在,请求出此时t的值;若不存在,请说明理由;
(3)若经过t秒后,恰好使矩形ABPF的面积与直角三角形BCQ的面积相等,求a的取值范围.
分析:(1)根据平行线分线段成比例定理求出PF,得出
=
,代入求出即可;
(2)连接BF、FQ,根据勾股定理求出即可;
(3)根据面积公式求出t,根据t、a的取值求出即可.
| BP |
| BC |
| PE |
| CQ |
(2)连接BF、FQ,根据勾股定理求出即可;
(3)根据面积公式求出t,根据t、a的取值求出即可.
解答:解:(1)∵EF∥AB,
∴△CEP∽△CAB,
∴
=
,
即
=
,
∴PE=
t,
∵EF∥CD,
∴△BPE∽△BCQ,
∴
=
,
即
=
,
解得t1=1,t2=0,
∵t>0,
∴t=1,
答:t的值是1秒.
(2)连接BF、FQ,
根据勾股定理得:BF2+FQ2=BQ2,
即42+(6-t)2+t2+(4-t)2=t2+62,
解得:t=2,t=8>4(舍去).
答:在运动过程中,存在某一时刻t,使得∠BFQ=90°,此时t的值是2秒.
(3)根据面积公式得:
at=4(a-t),
∴at=8(a-t),
∴(a+8)t=8a,
解得:t=
,
根据题意得:t≤4,
∴
≤4,
∴a≤8,
∵a>4,
∴4<a≤8.
答:a的取值范围是4<a≤8.
∴△CEP∽△CAB,
∴
| EP |
| AB |
| CP |
| BC |
即
| PE |
| 4 |
| t |
| 5 |
∴PE=
| 4 |
| 5 |
∵EF∥CD,
∴△BPE∽△BCQ,
∴
| BP |
| BC |
| PE |
| CQ |
即
| 5-t |
| 5 |
| ||
| t |
解得t1=1,t2=0,
∵t>0,
∴t=1,
答:t的值是1秒.
(2)连接BF、FQ,
根据勾股定理得:BF2+FQ2=BQ2,
即42+(6-t)2+t2+(4-t)2=t2+62,
解得:t=2,t=8>4(舍去).
答:在运动过程中,存在某一时刻t,使得∠BFQ=90°,此时t的值是2秒.
(3)根据面积公式得:
| 1 |
| 2 |
∴at=8(a-t),
∴(a+8)t=8a,
解得:t=
| 8a |
| a+8 |
根据题意得:t≤4,
∴
| 8a |
| a+8 |
∴a≤8,
∵a>4,
∴4<a≤8.
答:a的取值范围是4<a≤8.
点评:本题主要考查对勾股定理,相似三角形的性质和判定,平行线分线段成比例定理,矩形的性质等知识点的理解和掌握,能综合运用性质进行计算是解此题的关键.

练习册系列答案
相关题目
 如图,已知矩形DEFG内接于Rt△ABC,D在AB上,E、F在BC上,G在AC上,∠BAC=90°,AB=6cm,AC=8cm,
如图,已知矩形DEFG内接于Rt△ABC,D在AB上,E、F在BC上,G在AC上,∠BAC=90°,AB=6cm,AC=8cm, m/秒的速度移动,如果M、N两点同时出发,移动的时间为x秒(0≤x≤6).
m/秒的速度移动,如果M、N两点同时出发,移动的时间为x秒(0≤x≤6). 点A运动.
点A运动. (2012•宁德质检)如图,已知Rt△ABC,∠B=90°,AB=8,BC=6,把斜边AC平均分成n段,以每段为对角线作边与AB、BC平行的小矩形,则这些小矩形的面积和是( )
(2012•宁德质检)如图,已知Rt△ABC,∠B=90°,AB=8,BC=6,把斜边AC平均分成n段,以每段为对角线作边与AB、BC平行的小矩形,则这些小矩形的面积和是( ) 如图,已知矩形ABCD中AB:BC=3:1,点A、B在x轴上,直线y=mx+n(0<m<n<
如图,已知矩形ABCD中AB:BC=3:1,点A、B在x轴上,直线y=mx+n(0<m<n<