题目内容
9. 直线y=x+a与反比例函数y=$\frac{8}{x}$(x>0)的图象相交于A,与y轴相交于B,则OA2-OB2=16.
直线y=x+a与反比例函数y=$\frac{8}{x}$(x>0)的图象相交于A,与y轴相交于B,则OA2-OB2=16.
分析 把y=x+a代入y=$\frac{8}{x}$求出x2+ax=8,y=x+a与x轴交点B的坐标是(-a,0),设A的坐标是(x,y),求出OA2-OB2=x2+(x+a)2-a2=2(x2+ax),代入求出即可.
解答 解:把y=x+a代入y=$\frac{8}{x}$得:x+a=$\frac{8}{x}$,
即x2+ax=8,
y=x+a与x轴交点B的坐标是(-a,0),
设A的坐标是(x,y),
∴OA2-OB2
=x2+y2-a2
=x2+(x+a)2-a2
=2x2+2ax
=2(x2+ax)
=2×8
=16.
故答案为16.
点评 本题考查了一次函数和反比例函数的交点问题的应用,主要考查学生的计算能力的能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
4.若3x+1=a,3y-1=b,则3x+y=( )
| A. | a•b | B. | a+b | C. | 3a+b | D. | 3ab |
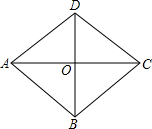 如图,菱形ABCD中,AC、BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线动动到C,动点N从B出发沿BD方向以1m/s匀速直线动动到D,若M、N同进出发,则出发后$\frac{5-\sqrt{2}}{2}$s或$\frac{5}{2}$s或$\frac{5+\sqrt{2}}{2}$s时,△MON的面积为$\frac{1}{4}$m2.
如图,菱形ABCD中,AC、BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线动动到C,动点N从B出发沿BD方向以1m/s匀速直线动动到D,若M、N同进出发,则出发后$\frac{5-\sqrt{2}}{2}$s或$\frac{5}{2}$s或$\frac{5+\sqrt{2}}{2}$s时,△MON的面积为$\frac{1}{4}$m2. 如图,△ABC中,AB=AC,∠BAC=90°,D为AB垂直平分线上一点,∠DAC=30°,求∠BCD的度数.
如图,△ABC中,AB=AC,∠BAC=90°,D为AB垂直平分线上一点,∠DAC=30°,求∠BCD的度数.