题目内容
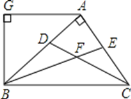
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,延长
的中点,延长![]() 至
至![]() ,使得
,使得![]() ,连接
,连接![]() 、
、![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)当![]() ,
,![]() 时,判断
时,判断![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)详见解析;(2)![]() 是底角为
是底角为![]() 的等腰三角形,解析解析
的等腰三角形,解析解析
【解析】
(1)由“ASA“可证△AEF≌△CED,可得AF=CD,根据邻边相等的平行四边形是菱形即可证明;
(2)由勾股定理可求AB的长,由中位线定理可求DF=DB=5,即可求解.
(1)∵AF∥CD,
∴∠EAF=∠ECD,
∵E是AC中点,
∴AE=EC,
在△AEF和△CED中,
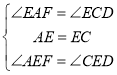
∴△AEF≌△CED(ASA),
∴AF=CD,
∴四边形AFCD是平行四边形,
∵∠ACB=![]() ,AD=DB,
,AD=DB,
∴CD=AD=BD,
∴四边形AFCD是菱形.
(2)∵∠ACB=![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴AB=![]()
∵点D,E分别是边AB,AC的中点,
∴BC=2DE,DB=![]() AB=5,
AB=5,
∵四边形AFCD是菱形,
∴DF=2DE=BC=5,
∴DF=DB,
∴△DFB是等腰三角形.

练习册系列答案
相关题目