��Ŀ����
����Ŀ���Ķ����⣺
��1����������ʽ���������и�ʽ�ķ������ʽ��ˣ�������ǵĻ������и�ʽ����ô����������ʽ�������������ʽ�����磺![]() ����������ʽ��
����������ʽ��![]() ��
��![]() ����������ʽ��
����������ʽ��![]() ��
��
��2����ĸ����������ĸ�������ֳơ���������ĸ����Ҳ���ǰѷ�ĸ�еĸ��Ż�ȥ��ָ�����������ʽ�з�ĸ�и��ţ���ôͨ�������ӡ���ĸͬ���Է�ĸ����������ʽ���ﵽȥ��ĸ�и��ŵ�Ŀ�ģ��磺![]() ��
��![]()
��������
��1����գ�![]() ����������ʽ��______����x��1��
����������ʽ��______����x��1��
��2��ֱ��д�����и�ʽ��ĸ�������Ľ����
��![]() _____����
_____����![]() ______��
______��
��3�����㣺![]() ��
��
���𰸡���1��![]() ����2����
����2����![]() ��
��![]() ����3��
����3��![]()
��������
��1������![]() �ɵô𰸣�
�ɵô𰸣�
��2���ٷ��ӷ�ĸͬ��![]() ���ٻ��ɣ�
���ٻ��ɣ�
�ڷ��ӷ�ĸͬ��![]() ���ٻ��ɣ�
���ٻ��ɣ�
��3�����÷�ĸ��������ʽ�ӻ������㼴�ɣ�
��1����![]()
��![]() ����������ʽ��
����������ʽ��![]()
�ʴ�Ϊ��![]()
��2����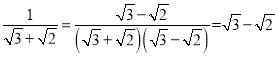
��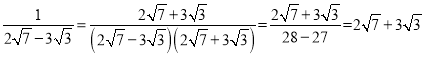
�ʴ�Ϊ����![]() ����
����![]() ��
��
��3��![]()
![]()
![]()

��ϰ��ϵ�д�
 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
�����Ŀ