Question

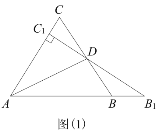
【题目】如图，已知的面积是12，，点，分别在边，上，在边上依次作了个全等的小正方形，，，，，则每个小正方形的边长为（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

设正方形的边长为x，根据正方形的性质以及相似三角形性质先求出相应情况下的正方形边长，然后进一步寻求规律即可.

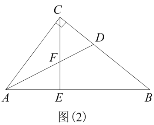
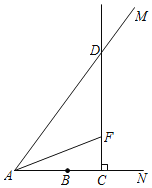
当作了1个正方形时，如图所示，

过A作AM⊥BC，垂足为M，交GH于N，

∴∠AMC=90°，

∵四边形EFGH为正方形，

∴GH∥BC，GH=GF，GF⊥BC，

∴∠AGH=∠B，∠ANH=∠AMC=90°，

∵∠GAH=∠BAC，

∴△AGH~△ABC，

∴AN:AM=GH:BC，

∵△ABC面积为12，BC为6，

∴，

∴AM=4，

设GH=，

∵GF=NM=GH，

∴AN=AMNM=AMGH=，

∴，

∴，

同理，当时，根据正方形性质可得：DN=2DE，

∴，

∴，

以此类推，当为第n个正方形时，每个小正方形边长为：，

故选：D.