题目内容
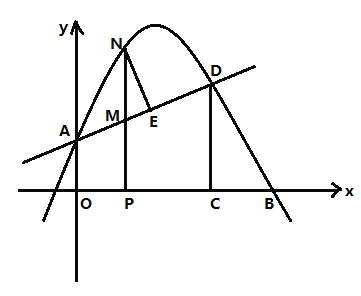
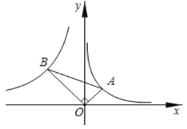
【题目】如图，已知抛物线y=ax2+bx-5的经过点（-2,-15）、点（2,1）．
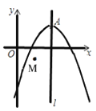
（1）求抛物线的表达式；
（2）请用配方法求抛物线顶点A的坐标；
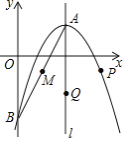
（3）已知点M坐标为（2，—1）．设动点P、Q分别在抛物线和对称轴
上，当以A，P，Q，M为顶点的四边形是平行四边形时，求P、Q两点的坐标．
【答案】（1）
；（2）顶点A（4，3）；（3）点
、
的坐标分别为
或
、
或
．
【解析】
（1）将点（-2,-15）、点（2,1）坐标代入y=ax2+bx-5即可求出a、b，从而得到抛物线解析式；
（2）将求出的二次函数解析式配成顶点式，即可得到顶点坐标；
（3）设点
、点
，分两种情况讨论：
是平行四边形的一条边或是平行四边形的对角线.
（1）将点（-2,-15）、点（2,1）坐标代入y=ax2+bx-5得：
解得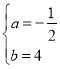
∴该抛物线的函数表达式为.
（2）
=-
（x2-8x）-5
=-（x-4）2+3
∴顶点A（4,3）.
（3）设点、点，
①当是平行四边形的一条边时，
，
，
解得：，
，
故点坐标为、的坐标为；
②当是平行四边形的对角线时，
，
，
解得：
，
，
故点的坐标为、的坐标为；
故点的坐标为或，的坐标为或．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
