题目内容
已知∠A为锐角且7sin2A-5sinA+cos2A=0,则tanA= .
【答案】分析:根据sin2A+cos2A=1,代入得出关于sinA的方程,求出sinA和cosA的值,再根据tanA= 代入求出即可.
代入求出即可.
解答:解:∵7sin2A-5sinA+cos2A=0,sin2A+cos2A=1,
∴7sin2A-5sinA+1-sin2A=0,
∴6sin2A-5sinA+1=0
∴(3sinA-1)(2sinA-1)=0,
∴3sinA-1=0,2sinA-1=0,
∴sinA= ,sinA=
,sinA= ,
,
∴cosA= =
= ,cosA=
,cosA= =
= ,
,
∴tanA= =
= =
= ,
,
tanA= =
= ,
,
故答案为: 或
或 .
.
点评:本题考查了同角的锐角三角函数值的应用,注意:sin2A+cos2A=1,tanA= .
.
 代入求出即可.
代入求出即可.解答:解:∵7sin2A-5sinA+cos2A=0,sin2A+cos2A=1,
∴7sin2A-5sinA+1-sin2A=0,
∴6sin2A-5sinA+1=0
∴(3sinA-1)(2sinA-1)=0,
∴3sinA-1=0,2sinA-1=0,
∴sinA=
 ,sinA=
,sinA= ,
,∴cosA=
 =
= ,cosA=
,cosA= =
= ,
,∴tanA=
 =
= =
= ,
,tanA=
 =
= ,
,故答案为:
 或
或 .
.点评:本题考查了同角的锐角三角函数值的应用,注意:sin2A+cos2A=1,tanA=
 .
. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则
,则 ;①
;① ,则
,则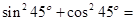 ;②
;② ,则
,则 .③
.③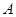 ,都有
,都有 .④
.④ 中,利用三角函数的定义及勾股定理对
中,利用三角函数的定义及勾股定理对 证明你的猜想
证明你的猜想
 且
且 ,求
,求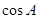 .
. ,则
,则 ; ①
; ①
 ,则
,则 ;
②
;
②  ,则
,则 .
③
.
③ .④
.④ 证明你的猜想;
证明你的猜想;
 且
且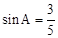 ,求
,求 .
.