题目内容
已知∠A为锐角且4sin2A-4sinAcosA+cos2A=0,则tanA=分析:先根据解一元二次方程的配方法,得出2sinA-cosA=0,再根据tanA的定义即可求出其值.
解答:解:由题意得:(2sinA-cosA)2=0,
解得:2sinA-cosA=0,2sinA=cosA,
∴tanA=
=
=0.5.
故答案为:0.5.
解得:2sinA-cosA=0,2sinA=cosA,
∴tanA=
| sinA |
| cosA |
| sinA |
| 2sinA |
故答案为:0.5.
点评:本题考查了锐角三角函数的定义及利用配方法解一元二次方程的知识,比较简单,注意锐角三角函数定义的掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则
,则 ;①
;① ,则
,则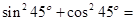 ;②
;② ,则
,则 .③
.③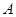 ,都有
,都有 .④
.④ 中,利用三角函数的定义及勾股定理对
中,利用三角函数的定义及勾股定理对 证明你的猜想
证明你的猜想
 且
且 ,求
,求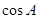 .
. ,则
,则 ; ①
; ①
 ,则
,则 ;
②
;
②  ,则
,则 .
③
.
③ .④
.④ 证明你的猜想;
证明你的猜想;
 且
且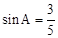 ,求
,求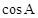 .
.