题目内容
9.若规定“$\root{n}{{a}^{m}}$=${a}^{\frac{m}{n}}$,m、n为整数,a-p=$\frac{1}{{a}^{p}}$,P为实数”,且有公式“(as)t=ast,s,t为有理数,a>0”,则当${a}^{\frac{1}{2}}$+${a}^{-\frac{1}{2}}$=3时,${a}^{\frac{3}{2}}$-${a}^{-\frac{3}{2}}$的值是±8$\sqrt{5}$.分析 把${a}^{\frac{3}{2}}$-${a}^{-\frac{3}{2}}$根据立方差公式,完全平方公式变形为±$\sqrt{({a}^{\frac{1}{2}+}{a}^{\frac{1}{2}})^{2}-4}$×[(${a}^{\frac{1}{2}}$+${a}^{-\frac{1}{2}}$)2-1],再把${a}^{\frac{1}{2}}$+${a}^{-\frac{1}{2}}$=3代入计算即可求解.
解答 解:当${a}^{\frac{1}{2}}$+${a}^{-\frac{1}{2}}$=3时,
${a}^{\frac{3}{2}}$-${a}^{-\frac{3}{2}}$
=(${a}^{\frac{1}{2}}$-${a}^{-\frac{1}{2}}$)(a+1+a-1)
=±$\sqrt{({a}^{\frac{1}{2}+}{a}^{\frac{1}{2}})^{2}-4}$×[(${a}^{\frac{1}{2}}$+${a}^{-\frac{1}{2}}$)2-1]
=±$\sqrt{9-4}$×[9-1]
=±8$\sqrt{5}$
故答案为:±8$\sqrt{5}$.
点评 考查了分数指数幂,实数的运算,关键是熟练掌握立方差公式,完全平方公式.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
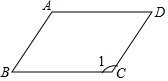 在四边形ABCD中,已知∠B=60°,∠1=120°,AB与CD平行吗?AD与BC平行吗?
在四边形ABCD中,已知∠B=60°,∠1=120°,AB与CD平行吗?AD与BC平行吗?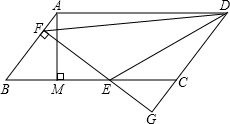 如图,?ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF.
如图,?ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF.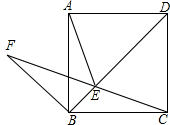 如图所示,在正方形ABCD的对角线BD上取一点E,使得∠BAE=15°,连接AE、CE,延长CE到F,连接BF,使得BC=BF.若AB=1,有下列结论:①AE=EC;②F到BC的距离为$\frac{\sqrt{2}}{2}$;③BE+EC=EF;④S△EBF=$\frac{\sqrt{3}}{12}$.其中正确结论的序号是①③④.
如图所示,在正方形ABCD的对角线BD上取一点E,使得∠BAE=15°,连接AE、CE,延长CE到F,连接BF,使得BC=BF.若AB=1,有下列结论:①AE=EC;②F到BC的距离为$\frac{\sqrt{2}}{2}$;③BE+EC=EF;④S△EBF=$\frac{\sqrt{3}}{12}$.其中正确结论的序号是①③④.