题目内容
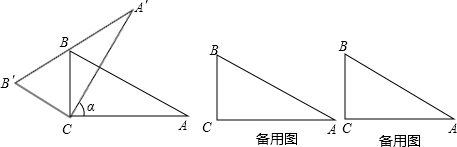
直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角α(0°<α<120°且α≠90°),得到Rt△A′B′C,
(1)如图,当A′B′边经过点B时,求旋转角α的度数;
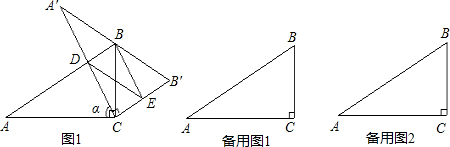
(2)在三角板旋转的过程中,边A′C与AB所在直线交于点D,过点 D作DE∥A′B′交CB′边于点E,连接BE.
①当0°<α<90°时,设AD=x,BE=y,求y与x之间的函数解析式及定义域;
②当 时,求AD的长.
时,求AD的长.

 解:(1)在Rt△ABC中,∵∠A=30°,
解:(1)在Rt△ABC中,∵∠A=30°,∴∠ABC=60°.
由旋转可知:B′C=BC,∠B′=∠ABC=60°,∠α=∠B′CB
∴△B′BC为等边三角形.
∴∠α=∠B′CB=60°.
(2)①当0°<α<90°时,点D在AB边上(如图).
∵DE∥A'B',
∴
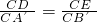 .
.由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE.
∴
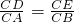 ,
,∴
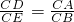 .
.∴△CAD∽△CBE;
∴
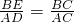 .
.∵∠A=30°
∴
 =
=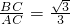 .
.∴
 (0<x<2)
(0<x<2)②当0°<α<90°时,点D在AB边上.
AD=x,BD=AB-AD=2-x,
∵DE∥A′B′,
∴
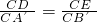 ,
,由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE.
∴
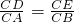 ,
,∴
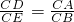 ,
,∴△CAD∽△CBE,
∴∠EBC=∠A=30°,又∠CBA=60°,
∴∠DBE=90°.
此时,
 .
.当S=
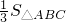 时,
时,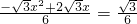 .
.整理,得x2-2x+1=0.
解得x1=x2=1,即AD=1.
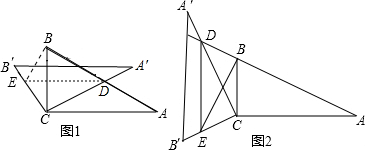
当90°<α<120°时,点D在AB的延长线上(如图).
仍设AD=x,则BD=x-2,∠DBE=90°,
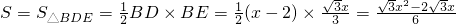 .
.当S=
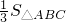 时,
时,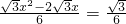 .
.整理,得x2-2x-1=0.
解得
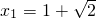 ,
,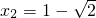 (负值,舍去).
(负值,舍去).即
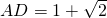 .
.综上所述:AD=1或
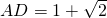 .
.分析:(1)由旋转的性质可得出∠α=∠B′CB=60°;
(2)①当0°<α<90°时,点D在AB边上(如图).根据平行线DE∥A'B'分线段成比例知
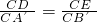 、及由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE由此证明△CAD∽△CBE;根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得
、及由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE由此证明△CAD∽△CBE;根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得 (0<x<2);
(0<x<2);②先求得△ABC的面积,再由△CAD∽△CBE,求得BE,分情况讨论:当点D在AB边上时,AD=x,BD=AB-AD=2-x;当点D在AB的延长线上时,AD=x,BD=x-2.
点评:本题主要考查旋转、全等三角形、解直角三角形、平行线分线段成比例等知识.解决本题的关键是结合图形,分类讨论.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
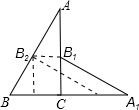 如图,直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板绕顶点C按顺时针方向旋转90°至△A1B1C的位置,沿CB向左平移使B1点落在△ABC的斜边AB上,点B1平移到点B2,则点B由B?B1?B2运动的路程是( )
如图,直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板绕顶点C按顺时针方向旋转90°至△A1B1C的位置,沿CB向左平移使B1点落在△ABC的斜边AB上,点B1平移到点B2,则点B由B?B1?B2运动的路程是( )A、(3π+3-
| ||||
B、(3π-3+
| ||||
C、(
| ||||
D、(
|
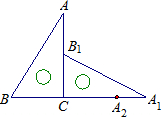 如图直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板ABC绕着直角顶点C顺时针方向旋转90°至△A1B1C1的位置,再沿CB向左平移使点B1落在△ABC的斜边AB上,点A1平移到点A2的位置,则点A?A1?A2运动的路径长度是
如图直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板ABC绕着直角顶点C顺时针方向旋转90°至△A1B1C1的位置,再沿CB向左平移使点B1落在△ABC的斜边AB上,点A1平移到点A2的位置,则点A?A1?A2运动的路径长度是