题目内容
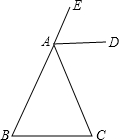如图，AD平分△ABC的外角∠EAC，且AD∥BC，试写出△ABC是等腰三角形的理由．
解：∵AD∥BC，
∴∠EAD=∠B，∠DAC=∠C，
∵∠EAD=∠DAC，
∴∠B=∠C，
∴△ABC是等腰三角形．
分析：根据平行线的性质可得到∠EAD=∠B，∠DAC=∠C，再根据角平分线的定义可推出∠B=∠C，根据有两个角相等的三角形是等腰三角形即可判定．
点评：此题主要考查等腰三角形的判定与平行线的性质的综合运用．
∴∠EAD=∠B，∠DAC=∠C，
∵∠EAD=∠DAC，
∴∠B=∠C，
∴△ABC是等腰三角形．
分析：根据平行线的性质可得到∠EAD=∠B，∠DAC=∠C，再根据角平分线的定义可推出∠B=∠C，根据有两个角相等的三角形是等腰三角形即可判定．
点评：此题主要考查等腰三角形的判定与平行线的性质的综合运用．
练习册系列答案
相关题目
16、如图，AD平分∠BAC，∠BAC+∠ACD=180°，E在AD上，BE的延长线交CD于F，连CE，且∠1=∠2，试说明AB=AC．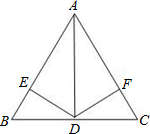
23、已知：如图，AD平分∠BAC，DE⊥AB，DF⊥AC，DB=DC，
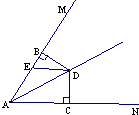23、如图，AD平分∠MAN，BD⊥AM，CD⊥AN，垂足分别为B、C
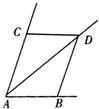18、如图，AD平分∠BAC，AC=AB，则△ABD≌△ACD．理由是：
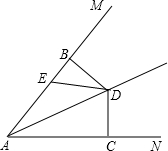如图，AD平分∠MAN，BD⊥AM，CD⊥AN，垂足分别为B、C，E为线段AB上一点，