Question

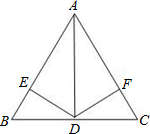23、已知：如图，AD平分∠BAC，DE⊥AB，DF⊥AC，DB=DC，
求证：△ABC是等腰三角形．

Answer 1

分析：欲证△ABC是等腰三角形，只要∠B=∠C即可，由已知条件，可通过三角形全等进行证明，答案可得．

解答：解：∵AD平分∠BAC（已知），
∴AD是△ABC顶角的角平分线（角平分线的定义），
∵DE⊥AB，DF⊥AC（已知），
∴DE=DF（角平分线的性质），
∵DB=DC（已知），
∴△BDE≌△CDF（HL）．
∴∠B=∠C（对应角相等），
∴△ABC是等腰三角形．

点评：本题考查了等腰三角形的判定及全等三角形的判定及性质；证明三角形全等是正确解答本题的关键．