题目内容
如图,直线y=-| 1 | 2 |
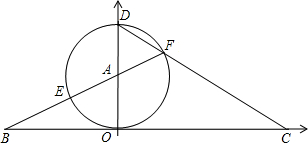 D为直径作⊙A交CD于F,FA的延长线交⊙A于E,交x轴于B.
D为直径作⊙A交CD于F,FA的延长线交⊙A于E,交x轴于B.(1)求点A的坐标;
(2)求△ADF的面积.
分析:(1)本题需先根据C、D两点都在直线y=-
x+4上,得出C、D的坐标,即可求出A点的坐标.
(2)连接OF,得出∠OFD=90°,从而得出△DOF∽△DCO,再设DF=x,则OF=2x,得出x的值,再根据面积公式即可求出答案.
| 1 |
| 2 |
(2)连接OF,得出∠OFD=90°,从而得出△DOF∽△DCO,再设DF=x,则OF=2x,得出x的值,再根据面积公式即可求出答案.
解答:解:(1)∵直线y=-
x+4分别与x轴,y轴交于点C、D,
∴C(8,0),D(0,4),
∵⊙A的直径为OD,
∴A(0,2);
(2)连接OF.
 ∵OD是圆O的直径,
∵OD是圆O的直径,
∴∠OFD=90°,
∴△DOF∽△DCO,
∴
=
,
∴
=
,
设DF=x,则OF=2x,
则x2+(2x)2=42=16,
∴x2=
,
∴△ODF=
×2x2
=
×2×
=
,
∴△ADF的面积=
△ODF=
.
| 1 |
| 2 |
∴C(8,0),D(0,4),
∵⊙A的直径为OD,
∴A(0,2);
(2)连接OF.
 ∵OD是圆O的直径,
∵OD是圆O的直径,∴∠OFD=90°,
∴△DOF∽△DCO,
∴
| DF |
| DO |
| OF |
| OC |
∴
| DF |
| 4 |
| OF |
| 8 |
设DF=x,则OF=2x,
则x2+(2x)2=42=16,
∴x2=
| 16 |
| 5 |
∴△ODF=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 16 |
| 5 |
=
| 16 |
| 5 |
∴△ADF的面积=
| 1 |
| 2 |
| 8 |
| 5 |
点评:本题主要考查了一次函数的综合,在解题时要能够灵活应用各个知识点,再把它们之间的关系联系起来是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,若平行四边形的面积是12,则△AOE与△DOF的面积和为( )
如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,若平行四边形的面积是12,则△AOE与△DOF的面积和为( )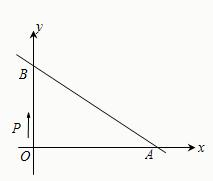 点出发,沿路线O→B→A以每秒1个单位长度的速度运动,到达A点时运动停止.
点出发,沿路线O→B→A以每秒1个单位长度的速度运动,到达A点时运动停止. 如图,直线
如图,直线 如图,直线
如图,直线