题目内容
 如图,两个反比例函数y1=
如图,两个反比例函数y1= 和y2=
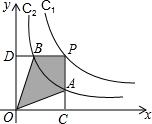
和y2= ,在第一象限内的图象依次是c1和c2,设点P在c1上,PC⊥x轴于点C,交c2于点A,PD⊥y轴于点D,交c2于点B,则四边形PAOB的面积为________.
,在第一象限内的图象依次是c1和c2,设点P在c1上,PC⊥x轴于点C,交c2于点A,PD⊥y轴于点D,交c2于点B,则四边形PAOB的面积为________.
2
分析:根据反比例函数的性质xy=k,即可得出正方形PCOD的面积,以及△ODB的面积与△OCA的面积,即可得出答案.
解答:∵两个反比例函数y= 和y=
和y= 在第一象限内的图象依次是C1和C2,
在第一象限内的图象依次是C1和C2,
∴正方形PCOD的面积为:xy=5,
∵△ODB的面积与△OCA的面积为xy= ,
,
∴四边形PAOB的面积为:5- -
- =2.
=2.
故答案为:2.
点评:此题主要考查了反比例函数系数k的几何意义,根据已知得出正方形PAOC的面积,以及△ODB的面积与△OCA的面积是解决问题的关键.
分析:根据反比例函数的性质xy=k,即可得出正方形PCOD的面积,以及△ODB的面积与△OCA的面积,即可得出答案.
解答:∵两个反比例函数y=
 和y=
和y= 在第一象限内的图象依次是C1和C2,
在第一象限内的图象依次是C1和C2,∴正方形PCOD的面积为:xy=5,
∵△ODB的面积与△OCA的面积为xy=
 ,
,∴四边形PAOB的面积为:5-
 -
- =2.
=2.故答案为:2.
点评:此题主要考查了反比例函数系数k的几何意义,根据已知得出正方形PAOC的面积,以及△ODB的面积与△OCA的面积是解决问题的关键.

练习册系列答案
相关题目
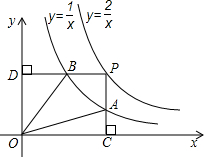 如图,两个反比例函数y=
如图,两个反比例函数y=| 2 |
| x |
| 1 |
| x |
| 2 |
| x |
| 1 |
| x |
| 1 |
| x |
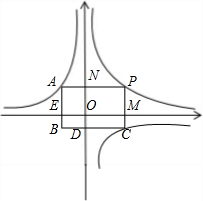 如图,两个反比例函数y=
如图,两个反比例函数y=| k1 |
| x |
| k2 |
| x |
| A、|k1-k2| | ||
B、
| ||
| C、|k1•k2| | ||
D、
|
 (2012•德州)如图,两个反比例函数
(2012•德州)如图,两个反比例函数 如图,两个反比例函数y=
如图,两个反比例函数y=