题目内容
5.如果将抛物线y=x2-2x-1向上平移,使它经过点A(0,3),那么所得新抛物线的表达式是y=x2-2x+3.分析 设平移后的抛物线解析式为y=x2-2x-1+b,把点A的坐标代入进行求值即可得到b的值.
解答 解:设平移后的抛物线解析式为y=x2-2x-1+b,
把A(0,3)代入,得
3=-1+b,
解得b=4,
则该函数解析式为y=x2-2x+3.
故答案是:y=x2-2x+3.
点评 本题考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.

练习册系列答案
相关题目
15.观察下列图案,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.某工程队有14名员工,他们的工种及相应每人每月工资如表所示:
现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差( )
| 工种 | 人数 | 每人每月工资/元 |
| 电工 | 5 | 7000 |
| 木工 | 4 | 6000 |
| 瓦工 | 5 | 5000 |
| A. | 变小 | B. | 不变 | C. | 变大 | D. | 无法确定 |
15. 如图,弦AB⊥OC,垂足为点C,连接OA,若OC=4,AB=6,则sinA等于( )
如图,弦AB⊥OC,垂足为点C,连接OA,若OC=4,AB=6,则sinA等于( )
 如图,弦AB⊥OC,垂足为点C,连接OA,若OC=4,AB=6,则sinA等于( )
如图,弦AB⊥OC,垂足为点C,连接OA,若OC=4,AB=6,则sinA等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
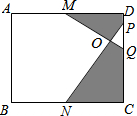 如图,在矩形ABCD中,M、N分别是边AD、BC的中点,点P、Q在DC边上,且PQ=$\frac{1}{4}$DC.若AB=16,BC=20,则图中阴影部分的面积是92.
如图,在矩形ABCD中,M、N分别是边AD、BC的中点,点P、Q在DC边上,且PQ=$\frac{1}{4}$DC.若AB=16,BC=20,则图中阴影部分的面积是92. 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.