题目内容
19.(1)解不等式组$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3(x-1)<8-x}\end{array}\right.$(2)解方程:$\frac{x-3}{x-2}$+1=$\frac{3}{2-x}$,并把解集在数轴上表示出来.
分析 (1)分别求出不等式组中两不等式的解集,找出解集的公共部分求出不等式组的解集,表示在数轴上即可;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1①}\\{1-3(x-1)<8-x②}\end{array}\right.$,
由①得:x≤1,
由②得:x>-2,
在数轴上表示出不等式组的解集为
∴不等式组的解集为-2<x≤1;
(2)方程两边同乘(x-2)得:x-3+x-2=-3,
解得:x=1,
经检验x=1是原方程的解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
相关题目
10. 下面数据是20位同学的身高(单位:cm):
下面数据是20位同学的身高(单位:cm):
156 154 161 158 164 150 163 160 159 155
159 161 157 168 163 159 165 164 158 153
(1)这组数据中,最大值与最小值的差是18;
(2)将这组数据分为5组:150≤x<154,154≤x<158,158≤x<162,162≤x<166,166≤x<170,则组距是4;
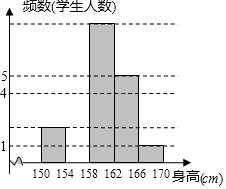
(3)完成下面频数分布表,并将频数分布直方图补充完整.
 下面数据是20位同学的身高(单位:cm):
下面数据是20位同学的身高(单位:cm):156 154 161 158 164 150 163 160 159 155
159 161 157 168 163 159 165 164 158 153
(1)这组数据中,最大值与最小值的差是18;
(2)将这组数据分为5组:150≤x<154,154≤x<158,158≤x<162,162≤x<166,166≤x<170,则组距是4;
(3)完成下面频数分布表,并将频数分布直方图补充完整.
| 身高分组 | 划记 | 频数 |
| 150≤x<154 | ||
| 154≤x<158 | ||
| 158≤x<162 | ||
| 162≤x<166 | 正 | 5 |
| 166≤x<170 |  ̄ | 1 |
4.如果-$\frac{1}{5}$x3yn与2xmy2是同类项,那么m,n的值分别是( )
| A. | m=3,n=2 | B. | m=0,n=2 | C. | m=1,n=4 | D. | m=2,n=1 |
9.若x>y,则下列式子中错误的是( )
| A. | x-2>y-2 | B. | 2-x>2-y | C. | x+2>y+1 | D. | $\frac{x}{3}$>$\frac{y}{3}$ |
 周末,某小组12名同学观看了电影《甲午风云》,其中8人买了甲票,4人买了乙票,总计用了200元,已知每张乙票比甲票售价多5元,设每张甲票的售价为x元,每张乙票的售价为y元.根据题意,可列方程组为$\left\{\begin{array}{l}{8x+4y=200}\\{y-x=5}\end{array}\right.$.
周末,某小组12名同学观看了电影《甲午风云》,其中8人买了甲票,4人买了乙票,总计用了200元,已知每张乙票比甲票售价多5元,设每张甲票的售价为x元,每张乙票的售价为y元.根据题意,可列方程组为$\left\{\begin{array}{l}{8x+4y=200}\\{y-x=5}\end{array}\right.$. 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF.
如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF.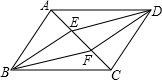 如图,四边形ABCD是平行四边形,且DE∥BF,分别交对角线AC于点E、F,连接EB,FD.
如图,四边形ABCD是平行四边形,且DE∥BF,分别交对角线AC于点E、F,连接EB,FD.