题目内容
15.先化简再求值:$\frac{x+1}{y}÷\frac{{{x^2}-1}}{y^2}$,其中:x=$\sqrt{2}$+1,y=$\sqrt{3}$.分析 先根据分式混合运算的法则把原式进行化简,再把x,y的值代入进行计算即可.
解答 解:原式=$\frac{x+1}{y}$•$\frac{{y}^{2}}{{x}^{2}-1}$
=$\frac{x+1}{y}$•$\frac{{y}^{2}}{(x+1)(x-1)}$
=$\frac{{{y^{\;}}}}{x-1}$,
当x=$\sqrt{2}$+1,y=$\sqrt{3}$时,原式=$\frac{{\sqrt{3}}}{{\sqrt{2}+1-1}}$=$\frac{{\sqrt{3}}}{{\sqrt{2}}}$=$\frac{{\sqrt{6}}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
11.在实数范围内,二次根式$\sqrt{x-5}$有意义的x的取值范围是( )
| A. | x≤5 | B. | x>5 | C. | x<5 | D. | x≥5 |
9.根据下表中的对应值,判断一元二次方程x2-4x+2=0的一个解的取值范围是0.5<x<1.
| x | 0 | 0.5 | 1 | 1.5 |
| x2-4x+2 | 2 | 0.25 | -1 | -1.75 |
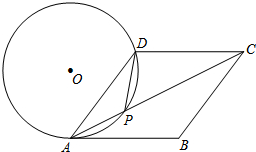 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.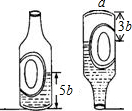 小聪量了自己喝的矿泉水瓶瓶底的直径为a厘米,瓶中水的高度为5b厘米,如图所示,他把矿泉水瓶颠倒过来测量了上面空瓶部分的高度为3b厘米(瓶子和瓶盖的厚度忽略不计),用a,b表示这个瓶子的容积为2πa2b立方厘米.
小聪量了自己喝的矿泉水瓶瓶底的直径为a厘米,瓶中水的高度为5b厘米,如图所示,他把矿泉水瓶颠倒过来测量了上面空瓶部分的高度为3b厘米(瓶子和瓶盖的厚度忽略不计),用a,b表示这个瓶子的容积为2πa2b立方厘米.