题目内容
10.|a|=4,b2=4,且|a+b|=a+b,那么a-b的值是2或6.分析 根据绝对值的性质求出a的值,根据平方根求出b的值,再根据|a+b|=a+b可知,a+b≥0,然后确定出a、b的值,再代入进行计算即可.
解答 解:∵|a|=4,
∴a=4或-4,
∵b2=4,
∴b=2或-2,
∵|a+b|=a+b,
∴a+b≥0,
∴a=4时,b=2,或a=4时,b=-2,
∴a-b=4-2=2,或a-b=4-(-2)=6,
综上所述,a-b的值是2或6.
故答案为:2或6.
点评 本题考查了有理数的混合运算,绝对值的性质,平方根的概念,根据题意求出a、b的值是解题的关键.

练习册系列答案
相关题目
1.有理数m、n互为相反数,x、y互为倒数,z的绝对值等于7,则m+n+5xy+z的值为( )
| A. | 12或-12 | B. | 2或-2 | C. | -12或2 | D. | 12或-2 |
18.下列各式中正确的是( )
| A. | ${({\frac{{2{x^2}}}{2y}})^3}=\frac{{2{x^6}}}{{2{y^3}}}$ | B. | ${({\frac{2a}{a+b}})^2}=\frac{{4{a^2}}}{{{a^2}+{b^2}}}$ | ||
| C. | ${({\frac{m+n}{m-n}})^3}=\frac{{{{(m+n)}^3}}}{{{{(m-n)}^3}}}$ | D. | ${({\frac{x-y}{x+y}})^2}=\frac{{{x^2}-{y^2}}}{{{x^2}+{y^2}}}$ |
15.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
(1)根据表中的数据,分别计算甲、乙两人的平均成绩:$\overline{x_甲}$=9环,$\overline{x_乙}$=9环.
(2)分别计算甲、乙六次测试成绩的方差;S甲2=$\frac{2}{3}$ 环2,S乙2=$\frac{4}{3}$环2.
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | |
| 甲 | 10 | 9 | 8 | 8 | 10 | 9 |
| 乙 | 10 | 10 | 8 | 10 | 7 | 9 |
(2)分别计算甲、乙六次测试成绩的方差;S甲2=$\frac{2}{3}$ 环2,S乙2=$\frac{4}{3}$环2.
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
2.木工师傅想利用木条制作一个直角三角形的工具,那么下列各组数据不符合直角三角形的三边长的是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 5,12,13 | D. | 13,16,18 |
19.如果两个相似三角形的相似比是1:2,那么这两个相似三角形的周长比是( )
| A. | 2:1 | B. | $1:\sqrt{2}$ | C. | 1:4 | D. | 1:2 |
20.如果两个三角形相似,其中一个三角形的两个内角分别为82°、53°,那么另一个三角形中最小的内角为 ( )
| A. | 82° | B. | 53° | C. | 45° | D. | 不能确定 |
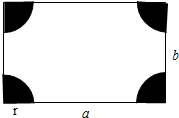 如图,在一长方形休闲广声场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
如图,在一长方形休闲广声场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.