题目内容
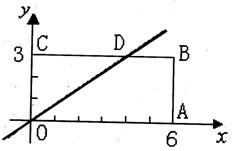
矩形![]() 在直角坐标系中的位置如图所示,
在直角坐标系中的位置如图所示,![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,直线
,直线![]() 与
与![]() 边相交于点
边相交于点![]() .(1)求点
.(1)求点![]() 的坐标;(2)若
的坐标;(2)若![]() 抛物
抛物![]() 线
线![]() 经过
经过![]() 、
、![]() 两点,试确定此抛物线的表达式;(3)设(2)中抛物线的对称轴与直线
两点,试确定此抛物线的表达式;(3)设(2)中抛物线的对称轴与直线![]() 交于点
交于点![]() ,点
,点![]() 为对称轴上一动点,以
为对称轴上一动点,以![]() 、
、![]() 、
、![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似,求符合条件的
相似,求符合条件的![]() 点的坐标.
点的坐标.

解:(1)由题知,直线![]() 与
与![]() 交于点
交于点![]() .
.
把![]() 代入
代入![]() 中得,
中得,![]()
![]()
(2)![]() 抛物线
抛物线![]() 经过
经过![]() 、
、![]() 两点,把
两点,把![]() ,
,![]() ;
;![]() ,
,![]() .分别代入
.分别代入![]() 中得,
中得,![]() 解之得
解之得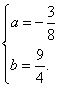
![]() 抛物线的解析式为:
抛物线的解析式为:![]() .
.
(3)抛物线的对称轴与![]() 轴的交点
轴的交点![]() ,符合条件,
,符合条件,
![]()
![]()
![]() ,
,![]() Rt△
Rt△![]() Rt△
Rt△![]() .
.
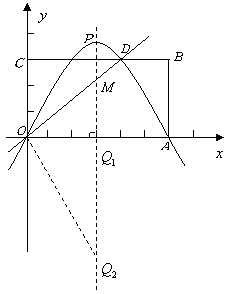
![]() ,该点坐标为
,该点坐标为![]() .
.
过点![]() 作
作![]() 的垂线交抛物线的对称轴于点
的垂线交抛物线的对称轴于点![]() ,
,
![]() 对称轴平行于
对称轴平行于![]() 轴,
轴,![]() ,
,
![]() Rt△
Rt△![]() Rt△
Rt△![]() .
.
在Rt△![]() 和Rt△
和Rt△![]() 中,
中,
![]() ,
,![]() ,
,
![]() Rt△
Rt△![]() Rt△
Rt△![]() .
.![]()
![]() ,
,
![]() 点
点![]() 位于第四象限,
位于第四象限,![]() .
.
因此,符合条件的点有两个,分别是![]() ,
,![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
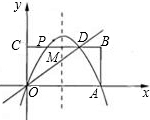 矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0)、C(0,3),直线y=
矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0)、C(0,3),直线y=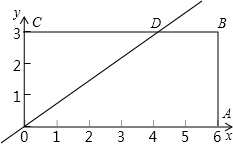 Q,以Q、O、M为顶点的三角形与△OCD相似?若存在,试求出符合条件的Q点的坐标;若不存在,试说明理由.
Q,以Q、O、M为顶点的三角形与△OCD相似?若存在,试求出符合条件的Q点的坐标;若不存在,试说明理由. (2011•黔东南州)矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(10,0)、C(0,3),直线
(2011•黔东南州)矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(10,0)、C(0,3),直线