��Ŀ����
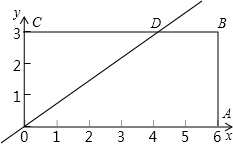
����OABC��ֱ������ϵ�е�λ����ͼ��ʾ��A��C���������ֱ�ΪA��6��0����C��0��3����ֱ��y=| 3 | 4 |
��1����������y=ax2+bx��a��0������D��A���㣬��ȷ���������ߵı���ʽ��
��2�����Ե�AΪԲ�ĵġ�A��ֱ��OD���У������A�İ뾶��
��3���裨1���������ߵĶԳ�����ֱ��OD���ڵ�M���ڶԳ������Ƿ���ڵ�
 Q����Q��O��MΪ��������������OCD���ƣ������ڣ����������������Q������ꣻ�������ڣ���˵�����ɣ�
Q����Q��O��MΪ��������������OCD���ƣ������ڣ����������������Q������ꣻ�������ڣ���˵�����ɣ�
��������1�������D�����꣬�ٰ�A��D�����������������y=ax2+bx������⼴�ɣ�
��2����A��AH��OD��H�����AH�ij����ǡ�A�İ뾶��
��3��������ڣ���OQ��QMʱ����Q1����OQ��OMʱ����Q2��ͨ��������֤�ж��Ƿ���ڣ�
��2����A��AH��OD��H�����AH�ij����ǡ�A�İ뾶��
��3��������ڣ���OQ��QMʱ����Q1����OQ��OMʱ����Q2��ͨ��������֤�ж��Ƿ���ڣ�
��� �⣺��1����
�⣺��1����
��D�������ΪD��4��3��
������y=ax2+bx����D��4��3����A��6��0�����ɵ�y=-
x2+
x
��2����CD=4��OC=3��OD=
=5��sin��CDO=
��
��A��AH��OD��H��
��AH=OAsin��DOA=6��
=
=3.6
�൱ֱ��OD���A����ʱ��r=3.6
��3���������ߵĶԳ�����x�ύ�ڵ�Q1�����Q1��������
��CB��OA��
���Q1OM=��ODC��
��Rt��Q1OM��Rt��CDO
�߶Գ���x=-
=3��
��Q1�������ΪQ1��3��0����
�ֹ�O��OD�Ĵ��߽������ߵĶԳ����ڵ�Q2�����Q2Ҳ��������
�߶Գ���ƽ����y�ᣬ
���Q2MO=��DOC��
��Rt��Q2MO��Rt��DOC
��Rt��Q2Q1O��Rt��DCO��Q1O=CO=3��
��Q2=��ODC��
��Rt��Q2Q1O��Rt��DCO��
��CD=Q1Q2=4��
��Q2λ�ڵ������ޣ���Q2��3��-4����
��ˣ����������ĵ����������ֱ���Q1��3��0����Q2��3��-4����
 �⣺��1����
�⣺��1����
|
������y=ax2+bx����D��4��3����A��6��0�����ɵ�y=-
| 3 |
| 8 |
| 9 |
| 4 |
��2����CD=4��OC=3��OD=
| 42+33 |
| 3 |
| 5 |
��A��AH��OD��H��
��AH=OAsin��DOA=6��
| 3 |
| 5 |
| 18 |
| 5 |
�൱ֱ��OD���A����ʱ��r=3.6
��3���������ߵĶԳ�����x�ύ�ڵ�Q1�����Q1��������
��CB��OA��
���Q1OM=��ODC��
��Rt��Q1OM��Rt��CDO
�߶Գ���x=-
| b |
| 2a |
��Q1�������ΪQ1��3��0����
�ֹ�O��OD�Ĵ��߽������ߵĶԳ����ڵ�Q2�����Q2Ҳ��������
�߶Գ���ƽ����y�ᣬ
���Q2MO=��DOC��
��Rt��Q2MO��Rt��DOC
��Rt��Q2Q1O��Rt��DCO��Q1O=CO=3��
��Q2=��ODC��
��Rt��Q2Q1O��Rt��DCO��
��CD=Q1Q2=4��
��Q2λ�ڵ������ޣ���Q2��3��-4����
��ˣ����������ĵ����������ֱ���Q1��3��0����Q2��3��-4����
�������������ؿ����˴���ϵ��������κ�������ʽ�����ν�ϵ���ѧ˼�뷽�����ۺ���ǿ������Ҫ��ߣ�

��ϰ��ϵ�д�
 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
�����Ŀ
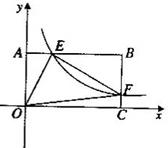

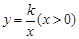 ��ͼ�����BC���ڵ�F��
��ͼ�����BC���ڵ�F��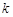 ��ֵ��
��ֵ��
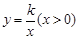 ��ͼ�����BC���ڵ�F��
��ͼ�����BC���ڵ�F��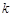 ��ֵ��
��ֵ��
 ��ͼ�����BC���ڵ�F.
��ͼ�����BC���ڵ�F.
 ����
���� ����k��ֵ.
����k��ֵ.