题目内容
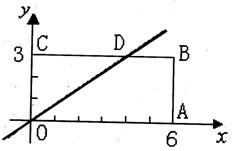
矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为![]() 、
、![]() ,直线
,直线![]() 与BC边相交于点D。
与BC边相交于点D。
(1)求点D的坐标;
(2)若抛物线![]() 经过D、A两点,试确定此抛物线的表达式;
经过D、A两点,试确定此抛物线的表达式;
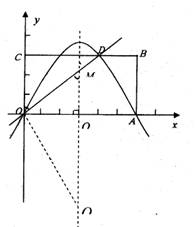
(3)设(2)中抛物线的对称轴与直线OD交于点M,点Q为对称轴上一动点,以Q、O、M为顶点的三角形与△OCD相似,求符合条件的Q点的坐标。
解:
(1)由题知,直线![]() 与BC交于点
与BC交于点![]()
把![]() 代入
代入![]() 中得,
中得,![]() ∴
∴![]()
(2)抛物线![]() 经过
经过![]() 、
、![]() 两点,把
两点,把![]() ,
,![]() ;
;![]() ,
,![]() 分别代入
分别代入![]() 中得
中得
![]() 解之得
解之得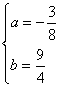
∴抛物线的解析式为:
(3)抛物线的对称轴与![]() 的交点
的交点![]() ,符合条件,
,符合条件,
∵CB∥OA,∠OM=∠CDO,
∴Rt△Q2MO∽Rt△DOC。
在Rt△Q2MO和Rt△DCO中,
![]() ,∠Q2=∠ODC,
,∠Q2=∠ODC,
∴Rt△Q2 Q1O≌Rt△DCO
∴CD= Q1Q2 =4
∵点Q2位于第四象限,∴![]()
因此,符合条件的点有两个,分别是![]() ,
,![]()

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
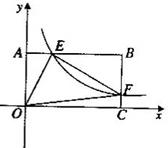

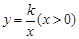 的图象与边BC交于点F。
的图象与边BC交于点F。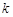 的值:
的值:
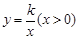 的图象与边BC交于点F。
的图象与边BC交于点F。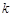 的值:
的值:
 的图象与边BC交于点F.
的图象与边BC交于点F.
 .且
.且 ,求k的值.
,求k的值.