题目内容
已知A,B,C三点在同一条数轴上.
(1)若点A,B表示的数分别为-4,2,且BC=
AB,则点C表示的数是 ;
(2)点A,B表示的数分别为m,n,且m<n.
①若AC-AB=2,求点C表示的数(用含m,n的式子表示);
②点D是这条数轴上的一个动点,且点D在点A的右侧(不与点B重合),当AD=2AC,BC=
BD,求线段AD的长(用含m,n的式子表示).
(1)若点A,B表示的数分别为-4,2,且BC=
| 1 |
| 2 |
(2)点A,B表示的数分别为m,n,且m<n.
①若AC-AB=2,求点C表示的数(用含m,n的式子表示);
②点D是这条数轴上的一个动点,且点D在点A的右侧(不与点B重合),当AD=2AC,BC=
| 1 |
| 4 |
考点:一元一次方程的应用,数轴
专题:
分析:(1)设点C表示的数是x.由BC=
AB列出方程|x-2|=
×(2+4),解方程即可;
(2)设点C表示的数是x.
①分两种情况进行讨论:Ⅰ)当点C在点B的右侧时,如图1所示,由AC-AB=2列出方程(x-m)-(n-m)=2,解方程即可;Ⅱ)当点C在点A的左侧时,如图2所示,由AC-AB=2列出方程(m-x)-(n-m)=2,解方程即可;
②由AD=2AC,可得点C在线段AD上或点C在点A的左侧.当动点D在线段AB上时,无论C在任何位置均不合题意;当动点D在点B的右侧时,分三种讨论进行情况:Ⅰ)当点C在线段BD的延长线上时,点C为线段AD的中点,当点C在线段BD上时,如图3所示,则AD=3n-3m;Ⅱ)当点C在线段AB上时,如图4所示,则AD=
n-
m;Ⅲ)当点C在点A左侧时,不合题意.
| 1 |
| 2 |
| 1 |
| 2 |
(2)设点C表示的数是x.
①分两种情况进行讨论:Ⅰ)当点C在点B的右侧时,如图1所示,由AC-AB=2列出方程(x-m)-(n-m)=2,解方程即可;Ⅱ)当点C在点A的左侧时,如图2所示,由AC-AB=2列出方程(m-x)-(n-m)=2,解方程即可;
②由AD=2AC,可得点C在线段AD上或点C在点A的左侧.当动点D在线段AB上时,无论C在任何位置均不合题意;当动点D在点B的右侧时,分三种讨论进行情况:Ⅰ)当点C在线段BD的延长线上时,点C为线段AD的中点,当点C在线段BD上时,如图3所示,则AD=3n-3m;Ⅱ)当点C在线段AB上时,如图4所示,则AD=
| 5 |
| 3 |
| 5 |
| 3 |
解答:解:(1)设点C表示的数是x.
∵点A,B表示的数分别为-4,2,且BC=
AB,
∴|x-2|=
×(2+4),
解得x=-1或5.
故答案为-1或5;
(2)设点C表示的数是x,由m<n,可得点A在点B的左侧,AB=n-m.
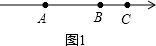 ①由AC-AB=2,得AC>AB.分两种情况:
①由AC-AB=2,得AC>AB.分两种情况:
Ⅰ)当点C在点B的右侧时,如图1所示,此时AC=x-m.
∵AC-AB=2,
∴(x-m)-(n-m)=2,
解得x=n+2.
∴点C表示的数是n+2;
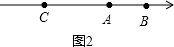 Ⅱ)当点C在点A的左侧时,如图2所示,此时AC=m-x.
Ⅱ)当点C在点A的左侧时,如图2所示,此时AC=m-x.
∵AC-AB=2,
∴(m-x)-(n-m)=2,
解得x=2m-n-2.
∴点C表示的数是2m-n-2.
综上,点C表示的数是n+2,2m-n-2;
②由AD=2AC,可得点C在线段AD上或点C在点A的左侧.
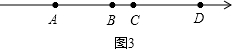 当动点D在线段AB上时,无论C在任何位置均不合题意;
当动点D在线段AB上时,无论C在任何位置均不合题意;
当动点D在点B的右侧时,分三种情况:
Ⅰ)当点C在线段BD的延长线上时,点C为线段AD的中点,
当点C在线段BD上时,如图3所示,
则AD=3n-3m;
 Ⅱ)当点C在线段AB上时,如图4所示,
Ⅱ)当点C在线段AB上时,如图4所示,
则AD=
n-
m;
Ⅲ)当点C在点A左侧时,不合题意.
综上所述,线段AD的长为3n-3m或
n-
m.
∵点A,B表示的数分别为-4,2,且BC=
| 1 |
| 2 |
∴|x-2|=
| 1 |
| 2 |
解得x=-1或5.
故答案为-1或5;
(2)设点C表示的数是x,由m<n,可得点A在点B的左侧,AB=n-m.
 ①由AC-AB=2,得AC>AB.分两种情况:
①由AC-AB=2,得AC>AB.分两种情况:Ⅰ)当点C在点B的右侧时,如图1所示,此时AC=x-m.
∵AC-AB=2,
∴(x-m)-(n-m)=2,
解得x=n+2.
∴点C表示的数是n+2;
 Ⅱ)当点C在点A的左侧时,如图2所示,此时AC=m-x.
Ⅱ)当点C在点A的左侧时,如图2所示,此时AC=m-x.∵AC-AB=2,
∴(m-x)-(n-m)=2,
解得x=2m-n-2.
∴点C表示的数是2m-n-2.
综上,点C表示的数是n+2,2m-n-2;
②由AD=2AC,可得点C在线段AD上或点C在点A的左侧.
 当动点D在线段AB上时,无论C在任何位置均不合题意;
当动点D在线段AB上时,无论C在任何位置均不合题意;当动点D在点B的右侧时,分三种情况:
Ⅰ)当点C在线段BD的延长线上时,点C为线段AD的中点,
当点C在线段BD上时,如图3所示,
则AD=3n-3m;
 Ⅱ)当点C在线段AB上时,如图4所示,
Ⅱ)当点C在线段AB上时,如图4所示,则AD=
| 5 |
| 3 |
| 5 |
| 3 |
Ⅲ)当点C在点A左侧时,不合题意.
综上所述,线段AD的长为3n-3m或
| 5 |
| 3 |
| 5 |
| 3 |
点评:本题考查了一元一次方程的应用,数轴,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
等腰三角形一腰上的高与另一腰的夹角为60°,则顶角的度数为( )
| A、30° |
| B、60° |
| C、60°或120° |
| D、30°或150° |
在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为
,把△EFO缩小,则点E的对应点E′的坐标是( )
| 1 |
| 2 |
| A、(-2,1) |
| B、(-8,4) |
| C、(-2,1)或(2,-1) |
| D、(-8,4)或(8,-4) |
如果多项式x2-mx+6分解因式的结果是(x-3)(x+n),那么m,n的值分别是( )
| A、m=-2,n=5 |
| B、m=2,n=5 |
| C、m=5,n=-2 |
| D、m=-5,n=2 |
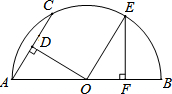 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( ) 如图,在△ABC中,BD平分∠ABC,∠ACE是△ABC的外角,CD平分∠ACE,∠A=50°,则∠D的度数为
如图,在△ABC中,BD平分∠ABC,∠ACE是△ABC的外角,CD平分∠ACE,∠A=50°,则∠D的度数为