题目内容
已知关于x的一元二次方程x2+4x+m+4=0的实数根是x1,x2.
(1)求m的取值范围.
当x1+x2﹣x1x2<﹣6,且m为整数时,求m的值.
解:(1)∵方程有实数根,
∴△≥0,
∴△=42﹣4×1×(m+4)=﹣4m≥0,
∴m≤0,
∴m的取值范围为m≤0;
由根与系数的关系得:x1+x2=﹣4,x1x2=m+4,
∵x1+x2﹣x1x2<﹣6,
∴﹣4﹣m﹣4<﹣6,
∴m>﹣2,由(1)知m≤0,
∵m为整数,
∴m=﹣1或0.

练习册系列答案
相关题目
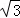 ≈1.7,结果保留整数).
≈1.7,结果保留整数).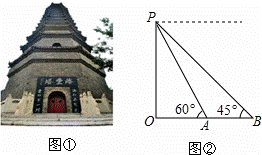
 )﹣2+(sin45°)0﹣
)﹣2+(sin45°)0﹣ +|﹣4|
+|﹣4|
 cm B. 4cm C.
cm B. 4cm C.  cm D.
cm D.  cm
cm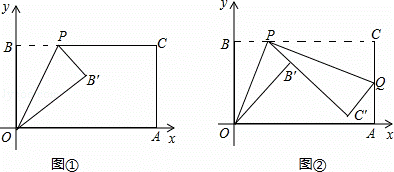

 B.
B.  C. 1 D.
C. 1 D.