题目内容
 如图,已知BC为⊙O的直径,A点在圆周上,AB=6,AC=8,AE平分∠BAC,求AE的长为
如图,已知BC为⊙O的直径,A点在圆周上,AB=6,AC=8,AE平分∠BAC,求AE的长为
- A.
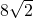
- B.
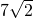
- C.

- D.

B
分析:过B作BN∥AE交CA于N,过A作AM⊥BC于M,连接OE,求出AN=AB,求出BZ和CZ,求出AM,EZ,根据勾股定理求出AZ和EZ即可.
解答: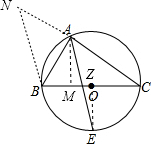
过B作BN∥AE交CA于N,过A作AM⊥BC于M,连接OE,
∵BC为直径,
∴∠BAC=90°,
∵AB=6,AC=8,由勾股定理得:BC=10,
由三角形面积公式得:AC×AB=BC×AM,
∴AM=4.8,
∵BN∥AE,
∴∠N=∠CAE,∠NBA=∠BAE,
∵AE平分∠BAC,
∴∠CAE=∠BAE,
∴∠N=∠NBA,
∴AB=AN,
∵BN∥AE,
∴ =
=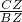 ,
,
∴ =
=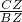 ,
,
∴ =
=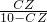 ,
,
CZ= ,BZ=10-
,BZ=10- =
= ,
,
∵AE平分∠BAC,
∴∠CAE=∠BAE,
∴弧CE=弧BE,
∴EO⊥BC,
∵OE=OC= BC=5,
BC=5,
∴ZO= -5=
-5= ,
,
由勾股定理得:EZ=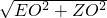 =
=
 ,
,
在Rt△ABM中,BM=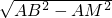 =
= ,
,
∴MZ= -
- =
= ,
,
在Rt△AMZ中,AZ=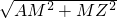 =
=
 ,
,
∴AE=AZ+EZ=
 +
+
 =7
=7 ,
,
故选B.
点评:本题考查了圆周角定理,勾股定理,角平分线性质,平行线分线段成比例定理的应用,主要考查学生的推理能力和计算能力.
分析:过B作BN∥AE交CA于N,过A作AM⊥BC于M,连接OE,求出AN=AB,求出BZ和CZ,求出AM,EZ,根据勾股定理求出AZ和EZ即可.
解答:

过B作BN∥AE交CA于N,过A作AM⊥BC于M,连接OE,
∵BC为直径,
∴∠BAC=90°,
∵AB=6,AC=8,由勾股定理得:BC=10,
由三角形面积公式得:AC×AB=BC×AM,
∴AM=4.8,
∵BN∥AE,
∴∠N=∠CAE,∠NBA=∠BAE,
∵AE平分∠BAC,
∴∠CAE=∠BAE,
∴∠N=∠NBA,
∴AB=AN,
∵BN∥AE,
∴
 =
=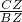 ,
,∴
 =
=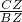 ,
,∴
 =
=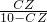 ,
,CZ=
 ,BZ=10-
,BZ=10- =
= ,
,∵AE平分∠BAC,
∴∠CAE=∠BAE,
∴弧CE=弧BE,
∴EO⊥BC,
∵OE=OC=
 BC=5,
BC=5,∴ZO=
 -5=
-5= ,
,由勾股定理得:EZ=
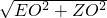 =
=
 ,
,在Rt△ABM中,BM=
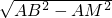 =
= ,
,∴MZ=
 -
- =
= ,
,在Rt△AMZ中,AZ=
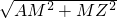 =
=
 ,
,∴AE=AZ+EZ=

 +
+
 =7
=7 ,
,故选B.
点评:本题考查了圆周角定理,勾股定理,角平分线性质,平行线分线段成比例定理的应用,主要考查学生的推理能力和计算能力.

练习册系列答案
相关题目
 如图,已知BC为⊙O的直径,过点C的弦CD平行于半径OA,若∠BCD=40°,则∠BAO的度数是( )
如图,已知BC为⊙O的直径,过点C的弦CD平行于半径OA,若∠BCD=40°,则∠BAO的度数是( )| A、20° | B、30° | C、40° | D、50° |

 14、如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,∠BAC≠90度.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平行四边形,则能拼出平行四边形
14、如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,∠BAC≠90度.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平行四边形,则能拼出平行四边形
 如图,已知BC为⊙O的直径,A点在圆周上,AB=6,AC=8,AE平分∠BAC,求AE的长为( )
如图,已知BC为⊙O的直径,A点在圆周上,AB=6,AC=8,AE平分∠BAC,求AE的长为( )