题目内容
【题目】以下是两张不同类型火车的车票(“![]() 次”表示动车,“
次”表示动车,“![]() 次”表示高铁):
次”表示高铁):
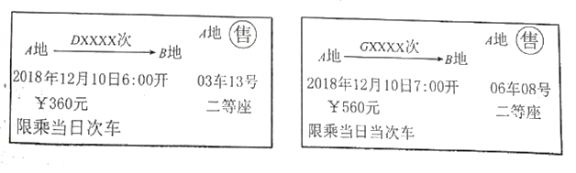
![]() 根据车票中的信息填空:该列动车和高铁是 向而行(填“相”或“同”).
根据车票中的信息填空:该列动车和高铁是 向而行(填“相”或“同”).
![]() 已知该动车和高铁的平均速度分别为
已知该动车和高铁的平均速度分别为![]() ,两列火车的长度不计.经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到2
,两列火车的长度不计.经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到2![]() .求
.求![]() 两地之间的距离.
两地之间的距离.
【答案】(1)同;(2)![]() 两地之间的距离是
两地之间的距离是![]() .
.
【解析】
(1)根据相向而行和同向而行的定义即可得出答案;
(2)先设出A、B两地之间的距离,再根据“高铁比动车早到2h”列出方程,解方程即可得出答案.
解:(1)∵动车和高铁的起始点和目的地均相同
∴动车和高铁是同向而行.
(2)设A、B两地之问的距离为xkm,
根据题意得:![]() ,
,
解得:![]() .
.
答:A、B两地之间的距离是1200km.

练习册系列答案
相关题目
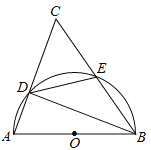
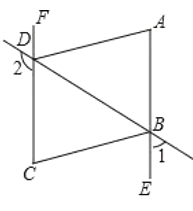
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是边
是边![]() 上一动点,连结
上一动点,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() .小梦根据学习函数的经验,对
.小梦根据学习函数的经验,对![]() 的面积与
的面积与![]() 的长度之间的关系进行了探究:
的长度之间的关系进行了探究:

(1)设![]() 的长度为
的长度为![]() ,
,![]() 的面积
的面积![]() ,通过取
,通过取![]() 边上的不同位置的点
边上的不同位置的点![]() ,经分析和计算,得到了
,经分析和计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 |
| 1 | 0 |
| 2 | 3 |
根据上表可知,![]() ______,
______,![]() ______.
______.
(2)在平面直角坐标系![]() 中,画出(1)中所确定的函数的图象.
中,画出(1)中所确定的函数的图象.

(3)在(1)的条件下,令![]() 的面积为
的面积为![]() .
.
①用![]() 的代数式表示
的代数式表示![]() .
.
②结合函数图象.解决问题:当![]() 时,
时,![]() 的取值范围为______.
的取值范围为______.