题目内容
9.已知下列等式:①22-12=3;②32-22=5;③42-32=7,…(1)请仔细观察前三个式子的规律,写出第④个式子:52-42=9;
(2)请你找出规律,写出第n个式子,并说明式子成立的理由:n2+2n+1-n2=2n+1.
利用(2)中发现的规律计算:1+3+5+7+…+2015+2017.
分析 (1)由等式左边两数的底数可知,两底数是相邻的两个自然数,右边为两底数的和,由此得出规律;
(2)等式左边减数的底数与序号相同,由此得出第n个式子;
(3)由3=22-12,5=32-22,7=42-32,…,将算式逐一变形,再寻找抵消规律.
解答 解:(1)依题意,得第④个算式为:52-42=9;
故答案为:52-42=9;
(2)根据几个等式的规律可知,第n个式子为:(n+1)2-n2=2n+1;
故答案为:n2+2n+1-n2=2n+1;
(3)由(2)的规律可知,
1+3+5+7+…+2015=1+(22-12)+(32-22)+(42-32)+…+(10092-10082)
=10092.
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算规律,利用规律解决问题.

练习册系列答案
相关题目
19.小华同学在学习整式乘法时发现,如果合理地使用乘法公式可以简化运算,于是如下计算题她是这样做的:
小禹看到小华的做法后,对她说:“你做错了,在第一步运用公式时出现了错误,你好好查一下.”小华仔细检查后自己找到了如下一处错误:

小禹看到小华的改错后说:“你还有错没有改出来.”
(1)你认为小禹说的对吗?对(对,不对)
(2)如果小禹说的对,那小华还有哪些错误没有改出来?请你帮助小华把第一步中的其它错误圈画出来并改正,再完成此题的解答过程.
| (2x-3y)2-(x-2y)(x+2y) =4x2-6xy+3y2-x2-2y2 第一步 =3x2-6xy+y2 第二步 |

小禹看到小华的改错后说:“你还有错没有改出来.”
(1)你认为小禹说的对吗?对(对,不对)
(2)如果小禹说的对,那小华还有哪些错误没有改出来?请你帮助小华把第一步中的其它错误圈画出来并改正,再完成此题的解答过程.
 如图,已知∠ABC=35°,∠C=47°,BD⊥AC,AE平分∠BAC,求∠BFE的度数.
如图,已知∠ABC=35°,∠C=47°,BD⊥AC,AE平分∠BAC,求∠BFE的度数. 我市某中学开设“生物第二课堂”,在校园内开辟出一块L型的空闲土地,准备进行植物种植研究,按如图所示的虚线分成了面积相等的两个梯形,这两个梯形的上底都是am,下底都是bm,高都是(b-a)m,请你算一算这块土地的面积是多少?并求出当a=20m,b=30m时这块土地的面积.
我市某中学开设“生物第二课堂”,在校园内开辟出一块L型的空闲土地,准备进行植物种植研究,按如图所示的虚线分成了面积相等的两个梯形,这两个梯形的上底都是am,下底都是bm,高都是(b-a)m,请你算一算这块土地的面积是多少?并求出当a=20m,b=30m时这块土地的面积.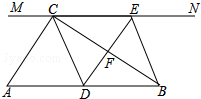 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
 如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号)
如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号) 如图,已知AB=AC=AD,且AD∥BC,求证:∠DAC=2∠D.
如图,已知AB=AC=AD,且AD∥BC,求证:∠DAC=2∠D. 如图,线段AB=16,以AB为直径的半圆上有一点C,连接BC并延长到点D,使DC=2BC,连接OD、AC交于点E,当∠B=2∠D时,线段OE的长为$\frac{4\sqrt{10}}{5}$.
如图,线段AB=16,以AB为直径的半圆上有一点C,连接BC并延长到点D,使DC=2BC,连接OD、AC交于点E,当∠B=2∠D时,线段OE的长为$\frac{4\sqrt{10}}{5}$.