Question

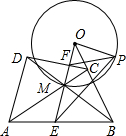设凸四边形ABCD的对角线AC、BD的交点为M，过点M作AD的平行线分别交AB、CD于点E、F，交BC的延长线于点O，P是以O为圆心OM为半径的圆上一点（位置如图所示），求证：∠OPF=∠OEP．

Answer 1

分析：作AD、BO的延长线相交于G，由OE∥GA，则

OF

OM

=

GD

GA

，再由

OM

OE

=

GD

GA

，从而得出

OF

OM

=

OM

OE

，由OM=OP，可以得出△POE∽△POF，从而证出∠OPF=∠OEP．

解答：证明：作AD、BO的延长线相交于G，
∵OE∥GA，
∴在△CGA中，

OF

OM

=

GD

GA

，
又在△BGA中，

OM

OE

=

GD

GA

，由此得

OF

OM

=

OM

OE

，而OM是⊙O的半径，
∴OM=OP，
∴

OF

OP

=

OP

OE

，
∴△POE∽△POF，
∴∠OPF=∠OEP．

点评：本题考查了相似三角形的判定和性质以及平行线分线段成比例定理，是一道综合题，难度较大．