题目内容
矩形OABC的顶点A(-8,0)、C(0,6) ,点D是BC边上的中点,抛物线![]() 经过A、D两点,如图所示.
经过A、D两点,如图所示.
1.求点D关于y轴的对称点![]() 的坐标及a、b的值;
的坐标及a、b的值;
2.在y轴上取一点P, 使PA+PD长度最短, 求点P的坐标;
3.将抛物线![]() 向下平移,记平移后点A的对应点为
向下平移,记平移后点A的对应点为![]() ,点D的对应点为
,点D的对应点为![]() ,当抛物线平移到某个位置时,恰好使得点O是y轴上到
,当抛物线平移到某个位置时,恰好使得点O是y轴上到![]() 两点距离之和
两点距离之和![]() 最短的一点,求此抛物线的解析式.
最短的一点,求此抛物线的解析式.

1.(1)由矩形的性质可知:B(-8,6)
∴D(-4,6); 点D关于y轴对称点D′(4,6)
将A(-8,0)、D(-4,6)代入![]() ,得:
,得:
 ;
;
2.设直线AD′的解析式为![]() ,则:
,则:
∴![]() 解得:
解得:
∴直线![]() 与y轴交于点(0,4),所以点P(0,4)
与y轴交于点(0,4),所以点P(0,4)
3.解法1:由于OP=4,故将抛物线向下平移4个单位时,有OA1+OD1最短;
∴ ![]() ,即此时的解析式为
,即此时的解析式为![]() ;
;
解法2:设抛物线向下平移了m个单位,则A1(-8,-m),D1(-4,6-m),
∴![]()
令直线![]() 为
为![]() ;
;

∵点O为使OA1+OD1最短的点,∴![]() ∴m=4,
∴m=4,
即将抛物线向下平移了4个单位;
∴![]() ,即此时的解析式为
,即此时的解析式为![]() .
.
解析:略

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 如图,在直角坐标系中,矩形OABC的顶点B的坐标为(15,6),直线
如图,在直角坐标系中,矩形OABC的顶点B的坐标为(15,6),直线 上是否存在点G,使得△CMG为等边三角形?若存在,求出点G的坐标;若不存在,请说明理由.
上是否存在点G,使得△CMG为等边三角形?若存在,求出点G的坐标;若不存在,请说明理由. 在x轴上,动点P从点C出发沿折线C→B→A运动,到达点A时停止,设点P运动的路程为m(0<m<14).
在x轴上,动点P从点C出发沿折线C→B→A运动,到达点A时停止,设点P运动的路程为m(0<m<14).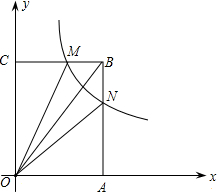 曲线y=
曲线y= (2012•东营)如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的
(2012•东营)如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的