题目内容
如图,已知二次函数y=-| 1 | 6 |
 在x轴上,动点P从点C出发沿折线C→B→A运动,到达点A时停止,设点P运动的路程为m(0<m<14).
在x轴上,动点P从点C出发沿折线C→B→A运动,到达点A时停止,设点P运动的路程为m(0<m<14).(1)求b,c的值;
(2)设直线OP在运动过程中扫过矩形的面积为S,求S关于m的函数关系式.
分析:(1)因为抛物线过A、B两点,所以将A、B两点坐标代入解析式,可列方程组解出系数的值;
(2)由图可知,直线OP在运动过程中过矩形的面积S,
①当0<m≤6时,图形为三角形;
②当6<m<14时,图形为梯形.
(2)由图可知,直线OP在运动过程中过矩形的面积S,
①当0<m≤6时,图形为三角形;
②当6<m<14时,图形为梯形.
解答:解:(1)将A(0,6),B(8,6)两点代入解析式得:
,
解得:b=
,c=6,
同时可得抛物线解析式为y=-
x2+
x+6;
(2)当①当0<m≤6时,图形为三角形,S=
OC•CP=
×8m=4m,
②当6<m<14时,扫过的图形为梯形,
于是S=
(OC+PB)•BC=
(8+m-6)•6=6+3m,
所以S=
.
|
解得:b=
| 4 |
| 3 |
同时可得抛物线解析式为y=-
| 1 |
| 6 |
| 4 |
| 3 |
(2)当①当0<m≤6时,图形为三角形,S=
| 1 |
| 2 |
| 1 |
| 2 |
②当6<m<14时,扫过的图形为梯形,
于是S=
| 1 |
| 2 |
| 1 |
| 2 |
所以S=
|
点评:本题主要考查了待定系数法求函数的解析式,是函数与矩形的性质相结合的问题,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
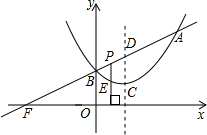 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.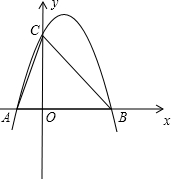
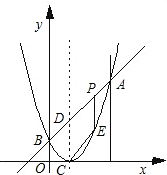 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.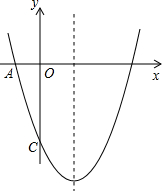 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).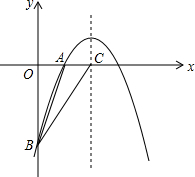 (2012•衡水一模)如图,已知二次函数
(2012•衡水一模)如图,已知二次函数