题目内容
 26、如图,AC∥DE,BC∥EF,AC=DE.求证:AF=BD.
26、如图,AC∥DE,BC∥EF,AC=DE.求证:AF=BD.分析:由AC∥DE,可知∠A=∠D,由BC∥EF,可知∠CBA=∠EFD.又因为AC=DE,∴△ABC≌△DFE,故AB=DF,AF-BD.
解答:证明:∵AC∥DE,
∴∠A=∠D,
∵BC∥EF,
∴∠CBA=∠EFD.
又∵AC=DE,
∴△ABC≌△DFE,
∴AB=DF,
∴AB-BF=DF-BF,
即AF=BD.
∴∠A=∠D,
∵BC∥EF,
∴∠CBA=∠EFD.
又∵AC=DE,
∴△ABC≌△DFE,
∴AB=DF,
∴AB-BF=DF-BF,
即AF=BD.
点评:本题考查的是平行线的性质及全等三角形的判定定理,比较简单.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 16、如图,AC⊥DE,垂足为O.∠B=40°,∠E=30°.则∠A=
16、如图,AC⊥DE,垂足为O.∠B=40°,∠E=30°.则∠A= 3、如图,AC∥DE,BD⊥BE,∠ABD=50°,则∠BED=( )
3、如图,AC∥DE,BD⊥BE,∠ABD=50°,则∠BED=( )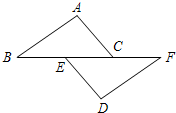 (1)已知:如图,AC∥DE,AC=DE,BE=CF,求证:∠B=∠F.
(1)已知:如图,AC∥DE,AC=DE,BE=CF,求证:∠B=∠F.
 如图,AC∥DE,AB平分∠DBC,∠A=70°,则∠CBE的度数为( )
如图,AC∥DE,AB平分∠DBC,∠A=70°,则∠CBE的度数为( )