题目内容
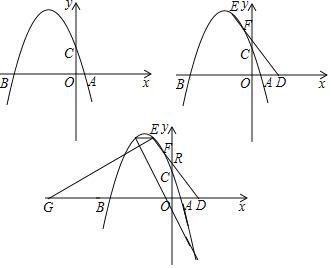
【题目】抛物线y=﹣![]() x+c交x轴于A、B两点(B在A左侧),交y轴于C,AB=10.
x+c交x轴于A、B两点(B在A左侧),交y轴于C,AB=10.
(1)求抛物线的解析式;
(2)在A点右侧的x轴上取点D,E为抛物线上第二象限内的点,连接DE交抛物线另外一点F,tan∠BDE=![]() ,DF=2EF,求E点坐标;
,DF=2EF,求E点坐标;
(3)在(2)的条件下,点G在x轴负半轴上,连接EG,EH∥AB交抛物线另外一点H,点K在第四象限的抛物线上,设DE交y轴于R,∠EHK=∠EGD+∠ORD,当HK=EG,求K点坐标.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+3;(2)E(﹣3,8);(3)K(﹣11,﹣8)
x+3;(2)E(﹣3,8);(3)K(﹣11,﹣8)
【解析】
(1)先根据函数关系式求出对称轴,由AB=10,求出点A的坐标,代入函数关系式求出c的值,即可解答;
(2)作EM⊥x轴,FN⊥x轴,FT⊥EM,得到四边形FTMN为矩形,由EM∥FN,FT∥BD.得到∠BDE=∠EFT,所以tan∠EFT=![]() ,设E(﹣3m,yE),F(﹣m,yF),可得
,设E(﹣3m,yE),F(﹣m,yF),可得![]() ,由y=﹣
,由y=﹣![]() x2﹣
x2﹣![]() x+3过点E、F,可得yE﹣yF=
x+3过点E、F,可得yE﹣yF=![]() m=(﹣3m2+8m+3)﹣(﹣
m=(﹣3m2+8m+3)﹣(﹣![]() m2+
m2+![]() m+3),可求m的值,代入解析式可求点E坐标;
m+3),可求m的值,代入解析式可求点E坐标;
(3)作EM⊥x轴,垂足为点M,过点K作KR⊥ED,与ED相交于点R,与x轴相交于点Q.再证明△EGM≌△EKR,求出点Q(﹣![]() ,0),点R(
,0),点R(![]() ,
,![]() )由待定系数法可求直线RQ的解析式为:y=
)由待定系数法可求直线RQ的解析式为:y=![]() x+
x+![]() ,设点K的坐标为(x,
,设点K的坐标为(x,![]() x+
x+![]() )代入抛物线解析式可得x=﹣11,即可求解.
)代入抛物线解析式可得x=﹣11,即可求解.
解:(1)由y=﹣![]() x2﹣
x2﹣![]() x+c,
x+c,
可得对称轴为x=﹣4
∵AB=10,
∴点A的坐标为(1,0),点B(﹣9,0)
∴﹣![]() ×12﹣
×12﹣![]() ×1+c=0,
×1+c=0,
∴c=3
∴抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+3;
x+3;
(2)如图2,作EM⊥x轴,垂足为点M,FN⊥x轴,垂足为点N,FT⊥EM,垂足为点T.

∴∠TMN=∠FNM=∠MTF=90°,
∴四边形FTMN为矩形,
∴EM∥FN,FT∥BD.
∴∠BDE=∠EFT,
∵tan∠BDE=![]() ,
,
∴tan∠EFT=![]() ,
,
设E(﹣3m,yE),F(﹣m,yF)
∴![]() ,
,
∵y=﹣![]() x2﹣
x2﹣![]() x+3过点E、F,
x+3过点E、F,
则yE﹣yF=![]() m=(﹣3m2+8m+3)﹣(﹣
m=(﹣3m2+8m+3)﹣(﹣![]() m2+
m2+![]() m+3),
m+3),
解得m=0(舍去)或m=1,
当m=1时,﹣3m=﹣3,
∴yE=﹣![]() ×(﹣3)2﹣
×(﹣3)2﹣![]() ×(﹣3)+3=8.
×(﹣3)+3=8.
∴E(﹣3,8).
(3)如图3,作EM⊥x轴,垂足为点M,过点K作KR⊥ED,与ED相交于点R,与x轴相交于点Q.
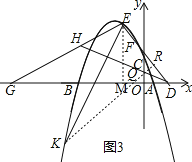
∵∠KER+∠EDH=90°,∠EGM+∠GEM=90°,∠EDH=∠EGM,
∴∠KER=∠GEM,
在△EGM和△EKR中,
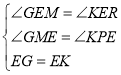
∴△EGM≌△EKR(AAS)
∴EM=ER=8,
∵tan∠BDE=![]() .
.
∴ED=10,
∴DR=2,
∴DQ=![]() ,
,
∴Q(﹣![]() ,0),
,0),
可求R(![]() ,
,![]() )
)
∴直线RQ的解析式为:y=![]() x+
x+![]() ,
,
设点K的坐标为(x,![]() x+
x+![]() )代入抛物线解析式可得x=﹣11
)代入抛物线解析式可得x=﹣11
∴K(﹣11,﹣8).

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案