Question

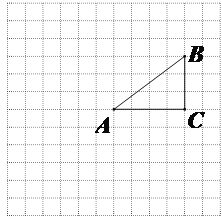
【题目】在△ABC中，∠ABC＝30°，AD⊥AB，交直线BC于点D，若AB＝4，CD＝1，则AC的长为_____．

Answer 1

【答案】或

【解析】

根据直角三角形的性质得到BD＝2AD，根据勾股定理求出BD，分两种情况计算即可．

解∵AD⊥AB，

∴∠BAD＝90°，

又∵∠ABC＝30°，

∴AD＝BD，

由勾股定理得，BD2＝AD2+AB2，即BD2＝（BD）2+（4）2

解得，BD＝8，

∴AD＝4，

过点A作AE⊥BC，垂足为E，

∵∠ABC＝30°，AB＝4，

∴AE＝2，

①当点D在线段BC上时，

∵∠ABC＝30°，∠BAD＝90°，

∴∠ADB＝60°，

∴∠DAE＝30°，

∴DE＝AD＝2，

∵CD＝1，

∴EC＝DE+DC＝2+1＝3，

∴AC＝＝＝，

②当点D在线段BC′的延长线上时，

EC'＝DE﹣DC＝2﹣1＝1

∴AC′＝＝＝，

故答案为：或．