Question

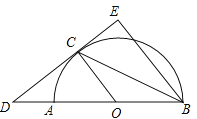
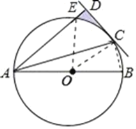
【题目】如图，AB为⊙O的直径，C为⊙O上一点，AD垂直于过点C的直线，垂足为D，且AC平分∠DAB，

（1）求证：DC是⊙O的切线；

（2）若⊙O的半径为2，AC＝2，求线段AD的长；

（3）在（2）的条件下，求图中阴影部分的面积（直接写出答案）．

Answer 1

【答案】（1）证明见解析；（2）AD=3；（3）

【解析】

（1）连接OC，由OA=OC可以得到∠OAC=∠OCA，然后利用角平分线的性质可以证明∠DAC=∠OCA，接着利用平行线的判定即可得到OC∥AD，然后就得到OC⊥CD，由此即可证明直线CD与⊙O相切于C点；

（2）连接BC，根据圆周角定理的推理得到∠ACB=90°，又∠DAC=∠OAC，由此可以得到△ADC∽△ACB，然后利用相似三角形的性质即可解决问题；

（3）设AD交⊙O于点E，连接OE，根据S阴=S梯形AOCD-S△AOE-S扇形COE计算即可.

（1）证明：连接OC，

∵OA＝OC

∴∠OAC＝∠OCA

∵AC平分∠DAB

∴∠DAC＝∠OAC

∴∠DAC＝∠OCA

∴OC∥AD

∵AD⊥CD，

∴OC⊥CD，

∴DC是⊙O的切线；

（2）连接BC，

∵AB为⊙O的直径，

∴∠ACB＝90°．

∵∠DAC＝∠OAC，∠ADC＝∠ACB＝90°，

∴△ADC∽△ACB，

∴，

∵⊙O的半径为2，AC＝2，

∴AD＝3；

（3）∵AD⊥CD，

∴，

∵OC∥AD，

∴S梯形AOCD＝，

在Rt△ABC中，AC＝2，AB＝4，

∴，

∴∠BAC＝30°，

∴∠BAD＝60°，

设AD交⊙O于点E，连接OE，

∵OA＝OE，

∴△AOE是等边三角形，

∴∠AOE＝60°，

∵OC∥AD，

∴∠AOC＝180°﹣∠BAD＝120°，

∴∠COE＝60°，

∴S阴＝S梯形AOCD﹣S△AOE﹣S扇形COE＝．