题目内容
已知抛物线y=
x2+x+c与x轴有交点.
(1)求c的取值范围;
(2)试确定直线y=cx+1经过的象限,并说明理由.
| 1 |
| 2 |
(1)求c的取值范围;
(2)试确定直线y=cx+1经过的象限,并说明理由.
(1)∵抛物线y=
x2+x+c与x轴有交点,
∴△=12-4×
c=1-2c≥0,解得c≤
;
(2)∵c≤
,
∴当0<c≤
时,直线y=cx+1经过一、二、三象限;
当c=0时,直线y=1经过一、二象限;
当c<0时,直线y=cx+1经过一、二、四象限.
| 1 |
| 2 |
∴△=12-4×
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵c≤
| 1 |
| 2 |
∴当0<c≤
| 1 |
| 2 |
当c=0时,直线y=1经过一、二象限;
当c<0时,直线y=cx+1经过一、二、四象限.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
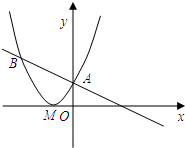 角形?若存在,求出点P的坐标;若不存在,请说明理由.
角形?若存在,求出点P的坐标;若不存在,请说明理由.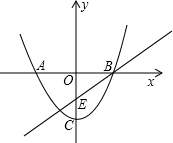 已知抛物线y=ax2+c与x轴交于A、B两点,与y轴交于C点,直线y=
已知抛物线y=ax2+c与x轴交于A、B两点,与y轴交于C点,直线y=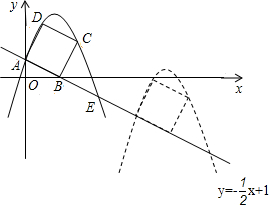
 如图,已知直线
如图,已知直线 +12x-19的顶点的横坐标是3,则a=________.
+12x-19的顶点的横坐标是3,则a=________.