题目内容
18.有一个边长为10尺的正方形池塘,一棵芦苇生长在它的正中央,高出水面的部分为1尺,如果把该芦苇的顶端沿水池边垂直的方向拉到岸边,发现芦苇顶端恰与水面齐平,则芦苇的长度是13尺.分析 找到题中的直角三角形,设水深为x尺,则芦苇长为(x+1)尺根据勾股定理可得方程x2+($\frac{10}{2}$)2=(x+1)2,再解方程即可.
解答 解:设水深为x尺,则芦苇长为(x+1)尺,
根据勾股定理得:x2+($\frac{10}{2}$)2=(x+1)2,
解得:x=12,
芦苇的长度=x+1=12+1=13(尺).
故答案为:13.
点评 本题考查主要考查了勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
8.如果x是最大的负整数,y是绝对值最小的整数,则-x2015+y的值是( )
| A. | 2015 | B. | -1 | C. | 1 | D. | -2015 |
6.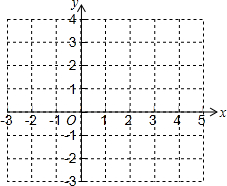 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.
(1)它与x轴交点的坐标为(1,0),(3,0),与y轴交点的坐标为(0,3);
(2)在坐标系中利用描点法画出此抛物线:
(3)根据图象说明:当x为何值时,函数y随着x的增大而增大?当x为何值时,函数y随着x的增大而减小?
 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.(1)它与x轴交点的坐标为(1,0),(3,0),与y轴交点的坐标为(0,3);
(2)在坐标系中利用描点法画出此抛物线:
| x | … | … | |||||
| y | … | … |
3. 如图,下列各组条件中,不能判定△ABC≌△DEF的是( )
如图,下列各组条件中,不能判定△ABC≌△DEF的是( )
 如图,下列各组条件中,不能判定△ABC≌△DEF的是( )
如图,下列各组条件中,不能判定△ABC≌△DEF的是( )| A. | AB=DE,∠A=∠D,AC=DF | B. | ∠B=∠E,AB=DE,AC=DE | ||
| C. | ∠A=∠D,AB=DE,∠B=∠E | D. | AB=DE,BC=EF,AC=DF |
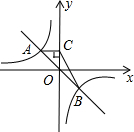 如图.函数y=-kx(k>0)与y=-$\frac{4}{x}$的图象交于A、B两点,过点A作AC垂直于y轴于点C,求△ABC的面积.
如图.函数y=-kx(k>0)与y=-$\frac{4}{x}$的图象交于A、B两点,过点A作AC垂直于y轴于点C,求△ABC的面积.