题目内容
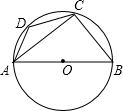如图，AB是⊙O的直径，C，D是⊙O上两点，∠BAC=40°，则∠D的度数为________度．
130
分析：根据直径所对的圆周角是直角得∠ACB=90°，则∠B=90°-40°=50°．根据圆内接四边形的对角互补求得∠D=180°-50=130°．
解答：∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠B=90°-40°=50°，
∴∠D=180°-50°=130°．
点评：此题运用了直径所对的圆周角是直角和圆内接四边形的对角互补的性质．
分析：根据直径所对的圆周角是直角得∠ACB=90°，则∠B=90°-40°=50°．根据圆内接四边形的对角互补求得∠D=180°-50=130°．
解答：∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠B=90°-40°=50°，
∴∠D=180°-50°=130°．
点评：此题运用了直径所对的圆周角是直角和圆内接四边形的对角互补的性质．
练习册系列答案
相关题目
8、如图，AB是铅直地竖立在坡角为30°的山坡上的电线杆，当阳光与水平线成60°角时，电线杆的影子BC的长度为4米，则电线杆AB的高度为（ ）
0.1平方米）
如图，AB是铅直地竖立在坡角为30°的山坡上的电线杆，当阳光与水平线成60°角时，电线杆的影子BC的长度为4米，则电线杆AB的高度为