题目内容
若am+n•an+1=a6,且m-2n=1,则mn+1的值是
- A.1
- B.3
- C.6
- D.9
D
分析:根据同底数幂的乘法的性质,同底数幂相乘,底数不变,指数相加计算即可列出方程组,求出m、n的值,从而求出mn+1的值.
解答:∵am+n•an+1=a6,
∴am+2n+1=a6,
∴m+2n+1=6,
∴ ,
,
解得: ,
,
∴mn+1=31+1=9.
故选D.
点评:主要考查同底数幂的乘法的性质,熟练掌握运算性质得出方程组,解出m、n的值是解题的关键.
分析:根据同底数幂的乘法的性质,同底数幂相乘,底数不变,指数相加计算即可列出方程组,求出m、n的值,从而求出mn+1的值.
解答:∵am+n•an+1=a6,
∴am+2n+1=a6,
∴m+2n+1=6,
∴
 ,
,解得:
 ,
,∴mn+1=31+1=9.
故选D.
点评:主要考查同底数幂的乘法的性质,熟练掌握运算性质得出方程组,解出m、n的值是解题的关键.

练习册系列答案
相关题目
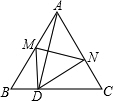 如图,将边长为6的正三角形ABC沿着MN折叠,使点A落在BC边上的D点处.
如图,将边长为6的正三角形ABC沿着MN折叠,使点A落在BC边上的D点处.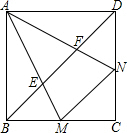 已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°
已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°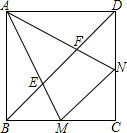 已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°
已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°