题目内容
求函数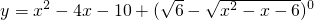 的最小值.
的最小值.
解:根据x2-x-6≥0且x2-x-6≠6时,函数才有意义,
解得:x≤-2且x≠-3或x≥3且x≠4,
此时函数y=x2-4x-9,
图象如图:

在x≤-2且x≠-3或x≥3且x≠4的范围内可知,
当x=3时,这个函数的最小值为-12.
分析:根据x2-x-6≥0且x2-x-6≠6时,函数才有意义,然后把函数化简即可求出最小值.
点评:本题考查了二次函数的最值及零指数幂,难度不大,关键是先求出x的范围,再根据图象法求出函数的最值.
解得:x≤-2且x≠-3或x≥3且x≠4,
此时函数y=x2-4x-9,
图象如图:

在x≤-2且x≠-3或x≥3且x≠4的范围内可知,
当x=3时,这个函数的最小值为-12.
分析:根据x2-x-6≥0且x2-x-6≠6时,函数才有意义,然后把函数化简即可求出最小值.
点评:本题考查了二次函数的最值及零指数幂,难度不大,关键是先求出x的范围,再根据图象法求出函数的最值.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数关系式为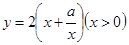
【探索研究】
(1)我们可以借鉴以前研究函数的经验,先探索函数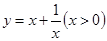 的图象和性质.
的图象和性质.
①填写下表,画出函数的图象;
|
x |
… |
|
|
|
1 |
2 |
3 |
4 |
… |
|
y |
… |
|
|
|
|
|
|
|
… |
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数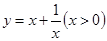 的最小值.
的最小值.
【解决问题】用上述方法解决“问题情境”中的问题,直接写出答案.
 22、已知函数y=x2-4x+1
22、已知函数y=x2-4x+1 ,即
,即 叫做正数
叫做正数 ,求函数
,求函数 ,则有
,则有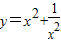 的最小值”提出各自的想法.甲说:“可以用配方法,把它配成
的最小值”提出各自的想法.甲说:“可以用配方法,把它配成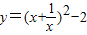 ,所以函数的最小值为-2”.乙说:“我也用配方法,但我配成
,所以函数的最小值为-2”.乙说:“我也用配方法,但我配成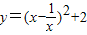 ,最小值为2”.你认为 (填写“甲对”,“乙对”,“甲,乙都对”或“甲乙都不对”)的.你还可以用 法等方法来解决.
,最小值为2”.你认为 (填写“甲对”,“乙对”,“甲,乙都对”或“甲乙都不对”)的.你还可以用 法等方法来解决.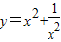 的最小值”提出各自的想法.甲说:“可以用配方法,把它配成
的最小值”提出各自的想法.甲说:“可以用配方法,把它配成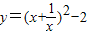 ,所以函数的最小值为-2”.乙说:“我也用配方法,但我配成
,所以函数的最小值为-2”.乙说:“我也用配方法,但我配成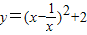 ,最小值为2”.你认为 (填写“甲对”,“乙对”,“甲,乙都对”或“甲乙都不对”)的.你还可以用 法等方法来解决.
,最小值为2”.你认为 (填写“甲对”,“乙对”,“甲,乙都对”或“甲乙都不对”)的.你还可以用 法等方法来解决.

