题目内容
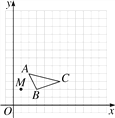
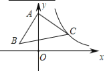
【题目】如图,在![]() 中,
中,![]() ,顶点
,顶点![]() 在
在![]() 轴上,顶点
轴上,顶点![]() 在反比例函数
在反比例函数![]() 的图象上,已知点
的图象上,已知点![]() 的纵坐标是 3,则经过点
的纵坐标是 3,则经过点![]() 的反比例函数的解析式为_____________
的反比例函数的解析式为_____________
【答案】![]()
【解析】
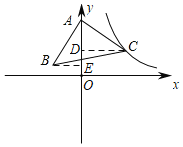
过C作CD⊥y轴于D,过B作BE⊥y轴于E,即可得到△ABE≌△CAD,依据全等三角形的性质以及点C的坐标,即可得到点B的坐标,进而得出经过点B的反比例函数的解析式.
如图所示,过C作CD⊥y轴于D,过B作BE⊥y轴于E,则∠CDA=∠AEB=90°,
又∵∠BAC=90°,
∴∠BAE+∠CAD=∠ACD+∠CAD=90°,
∴∠BAE=∠ACD,
又∵AB=CA,
∴△ABE≌△CAD(AAS),
又∵顶点C在反比例函数![]()
的图象上,点C的纵坐标为3,
∴点C的横坐标为4,
∴CD=4=AE,OD=3,
∴Rt△ACD中,AD= ![]()
= ![]() =2,
=2,
∴BE=AD=2,AO=AD+DO=2+3=5,
∴OE=AO-AE=5-4=1,
∴B(-2,1),
∴经过点B的反比例函数的解析式为![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目