题目内容
如图,矩形OABC的边OA在x轴上,OC边在y轴上,OA=8,OC=6,过点C与对角线OB 垂直的直线l,交x轴于P,
垂直的直线l,交x轴于P,
(1)求直线l的解析式及P点的坐标;
(2)若点P沿x轴的正方向以1单位/s的速度移动,直线l也随之移动,且l∥OB,设直线分矩形部分面积为y,求y与P点移动时间x的函数关系式;
(3)若点P在(2)的情况下移动的同时,直线l上有一点M,从P点出发以1单位/s的速度沿直线l向上移动,求以M为圆心,半径为1的圆与矩形四条边所在直线相切的时间x的值.
解:(1)B的坐标是(8,6),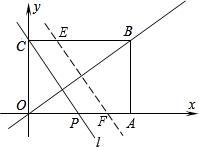
设直线L的解析式是y=kx,则6=8k,解得:k= ,
,
则直线OB的解析式是y= x,
x,
则直线l的一次项系数是:- ,设直线l的解析式是y=-
,设直线l的解析式是y=- x+b,
x+b,
把C的坐标(0,6)代入解析式得:6=b,
则l的解析式是:y=- x+6,设y=0,解得:x=
x+6,设y=0,解得:x= ,则P的坐标是(
,则P的坐标是( ,0);
,0);
(2)当P在A或A的左边时,即0≤x≤ 时:
时:
点P沿x轴的正方向以1单位/s的速度移动,x秒后到F点,则FA=8- -x=
-x= ,设直线l与BC的交点是E,则BE=8-x,四边形ABEP是直角梯形,
,设直线l与BC的交点是E,则BE=8-x,四边形ABEP是直角梯形,
则y= (AP+BE)•AB=
(AP+BE)•AB= (
( +8-x)×6=-6x+
+8-x)×6=-6x+ ;
;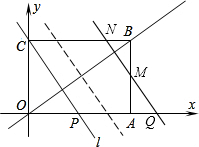
当 <x≤8时,设直线l与AB交于点M,与BC交于点N.交x轴与Q.
<x≤8时,设直线l与AB交于点M,与BC交于点N.交x轴与Q.
则AQ=x- ,
,
△OPC∽△AQM,
则 ,则AM=
,则AM=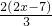 ,BM=6-
,BM=6-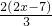 =
=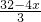 ,
,
BN=x,
则y= BN•BM=
BN•BM= x×
x×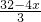 =
=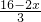 .
.
当x>8是,直线l与矩形不相交.
(3)在直角△OPC中,PC=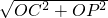 =
= ,
,
设M点运动x秒,则M的横坐标是: +x,
+x,
M的纵坐标是: x,则M的坐标是:(
x,则M的坐标是:( +x,
+x, x),
x),
当圆与OA相切时: x=1,解得:x=
x=1,解得:x= ;
;
当圆与OC相切时, +x=1,解得:x=-
+x=1,解得:x=- ,(舍去);
,(舍去);
当圆与AB相切时:8-( +x)=1或(
+x)=1或( +x)-8=1,解得:x=
+x)-8=1,解得:x= 或
或 ;
;
当圆与BC相切时,6- x=1或
x=1或 x-6=1,解得:x=
x-6=1,解得:x= 或
或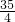 .
.
分析:(1)首先求得OB的解析式,根据直线l与OB垂直,即可求得直线l的解析式的一次项系数,再根据待定系数法即可求得直线l的解析式,求得P的坐标;
(2)分当P在A或A的左边时,即0≤x≤ 或当
或当 <x≤8以及x>8三种情况进行讨论,分别利用直角梯形的面积公式,以及直角三角形的面积公式即可求得函数解析式;
<x≤8以及x>8三种情况进行讨论,分别利用直角梯形的面积公式,以及直角三角形的面积公式即可求得函数解析式;
(3)首先利用时间x表示出M的坐标,然后根据圆与直线相交的条件:圆心到直线的距离等于圆的半径,分情况进行讨论,即可求得x的值.
点评:本题考查了待定系数法求函数的解析式,直线与圆的位置关系,正确求得M的坐标是关键.

设直线L的解析式是y=kx,则6=8k,解得:k=
 ,
,则直线OB的解析式是y=
 x,
x,则直线l的一次项系数是:-
 ,设直线l的解析式是y=-
,设直线l的解析式是y=- x+b,
x+b,把C的坐标(0,6)代入解析式得:6=b,
则l的解析式是:y=-
 x+6,设y=0,解得:x=
x+6,设y=0,解得:x= ,则P的坐标是(
,则P的坐标是( ,0);
,0);(2)当P在A或A的左边时,即0≤x≤
 时:
时:点P沿x轴的正方向以1单位/s的速度移动,x秒后到F点,则FA=8-
 -x=
-x= ,设直线l与BC的交点是E,则BE=8-x,四边形ABEP是直角梯形,
,设直线l与BC的交点是E,则BE=8-x,四边形ABEP是直角梯形,则y=
 (AP+BE)•AB=
(AP+BE)•AB= (
( +8-x)×6=-6x+
+8-x)×6=-6x+ ;
;
当
 <x≤8时,设直线l与AB交于点M,与BC交于点N.交x轴与Q.
<x≤8时,设直线l与AB交于点M,与BC交于点N.交x轴与Q.则AQ=x-
 ,
,△OPC∽△AQM,
则
 ,则AM=
,则AM=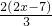 ,BM=6-
,BM=6-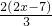 =
=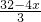 ,
,BN=x,
则y=
 BN•BM=
BN•BM= x×
x×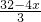 =
=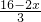 .
.当x>8是,直线l与矩形不相交.
(3)在直角△OPC中,PC=
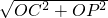 =
= ,
,设M点运动x秒,则M的横坐标是:
 +x,
+x,M的纵坐标是:
 x,则M的坐标是:(
x,则M的坐标是:( +x,
+x, x),
x),当圆与OA相切时:
 x=1,解得:x=
x=1,解得:x= ;
;当圆与OC相切时,
 +x=1,解得:x=-
+x=1,解得:x=- ,(舍去);
,(舍去);当圆与AB相切时:8-(
 +x)=1或(
+x)=1或( +x)-8=1,解得:x=
+x)-8=1,解得:x= 或
或 ;
;当圆与BC相切时,6-
 x=1或
x=1或 x-6=1,解得:x=
x-6=1,解得:x= 或
或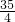 .
.分析:(1)首先求得OB的解析式,根据直线l与OB垂直,即可求得直线l的解析式的一次项系数,再根据待定系数法即可求得直线l的解析式,求得P的坐标;
(2)分当P在A或A的左边时,即0≤x≤
 或当
或当 <x≤8以及x>8三种情况进行讨论,分别利用直角梯形的面积公式,以及直角三角形的面积公式即可求得函数解析式;
<x≤8以及x>8三种情况进行讨论,分别利用直角梯形的面积公式,以及直角三角形的面积公式即可求得函数解析式;(3)首先利用时间x表示出M的坐标,然后根据圆与直线相交的条件:圆心到直线的距离等于圆的半径,分情况进行讨论,即可求得x的值.
点评:本题考查了待定系数法求函数的解析式,直线与圆的位置关系,正确求得M的坐标是关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
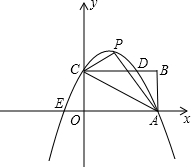 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA= (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2 如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是
如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是